Solution VI by Tom Verhoeff

Triangles with Equal Area VI

Here is Problem 4 from the IMO 2007:

In triangle ABC the bisector of angle BCA intersects the circumcircle again at R, the perpendicular bisector of BC at P, and the perpendicular bisector of AC at Q. The midpoint of BC is K and the midpoint of AC is L. Prove that the triangles RPK and RQL have the same area.

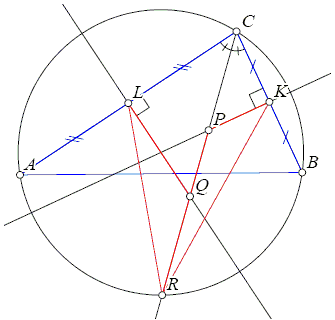
Solution below is an adaptation of that by Tom Verhoeff.

Using the similarity of triangles CPK and CQL and notation a = PR, b = RQ, c = CR, KS is the altitude at K, LT is the altitude at L, the required identity Area(RPK) = Area(RQL) is transformed sequentially:

Area(RPK) = Area(RQL)
RP · KS / 2 = RQ · LT / 2
RP / RQ = LT / KS
RP / RQ = CQ / CP
RP / RQ = (CR - RQ) / (CR - RP)
a : b = (c - b) : (c - a)
a(c - a) = b(c - b)
a(c - a) - b(c - b) = 0
(a - b)c - a² + b² = 0
(a - b)(c - (a + b)) = 0
Either a = b or c = a + b, but a and b are independent
CR = RP + RQ but also
CR = RP + CP so that
RQ = CP.

Therefore, it suffices to prove RQ = CP. For that purpose, we introduce the line through the circumcenter M perpendicular to angle bisector CR. Now, reflect ΔABC in this line to obtain ΔA'B'R.

Triangles ABC and A'B'R have the same circumcircle, since the reflection line passes through the circumcenter. Sides AC and B'R are parallel, because of equal angles with CR. Similarly, sides BC and A'R are parallel. The perpendicular bisector of B'R passes through the circumcenter M and is perpendicular to AC. Hence, the perpendicular bisectors of AC and B'R are the same. Consequently, Q is the reflection of P and, thus, indeed RQ = CP.

2007 IMO, Problem 4

71548409