A Property of Altitudes

Tran Quang Hung has observed the following property of altitudes in $\Delta ABC$ that generalizes a well-known identity that holds in right triangles:

(1)

$\displaystyle\frac{1}{AH^{2}_{a}}=\frac{1}{AB^2}+\frac{1}{AC^2},$

$H_a$ being the foot of the altitude from $A,$ as common. $H_b$ and $H_c$ are defined similarly.

$\displaystyle\frac{1}{H_{a}H_{b}\cdot H_{a}H_{c}}=\frac{1}{BH_{c}\cdot BA}+\frac{1}{CH_{b}\cdot CA}.$

The proof is based on two observations (I'll use a PWW approach with another page in mind):

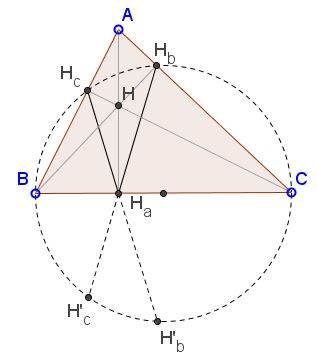
circles with sides of triangle as diameter, II

(2)

$BH_{a}\cdot CH_{a} = H_{a}H_{b}\cdot H_{a}H_{c}.$

And also

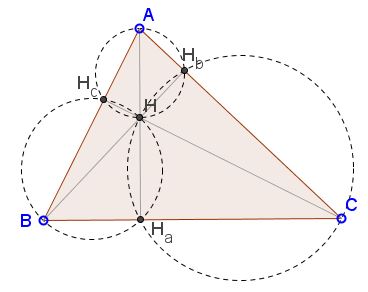
three cyclic quadrilaterals

(3)

$\begin{align} BH_{a}\cdot BC &=BH_{c}\cdot BA,\\ CH_{b}\cdot CA &=CH_{a}\cdot CB. \end{align}$

We thus have

$\begin{align}\displaystyle \frac{1}{BH_{c}\cdot BA}+\frac{1}{CH_{b}\cdot CA} &= \frac{1}{BH_{a}\cdot BC}+\frac{1}{CH_{a}\cdot CB}\\ &= \frac{BH_{a}+CH_{a}}{BH_{a}\cdot\cdot CH_{a}\cdot CB}\\ &= \frac{BC}{BH_{a}\cdot CH_{a}\cdot CB}\\ &= \frac{1}{BH_{a}\cdot CH_{a}}\\ &= \frac{1}{H_{a}H_{b}\cdot H_{a}H_{c}}. \end{align}$

Obviously, this reduces to (1) when $\angle BAC = 90^{\circ}.$

73176959