Chasles' Theorem, a Simple Proof

Chasles' theorem that, for four points on a non-degenerate conic, the cross-ratio of the pencil of four lines from a fifth point of the conic to the given points does not depend on the choice of the fifth point. The theorem is obviously of projective nature: it is stated for conics and makes an assertion about cross-ratios - an invariant under projective transformations. However, it has a very simple proof that is based on a common feature of inscribed angles subtending the same arc in a cricle: such angles are equal.

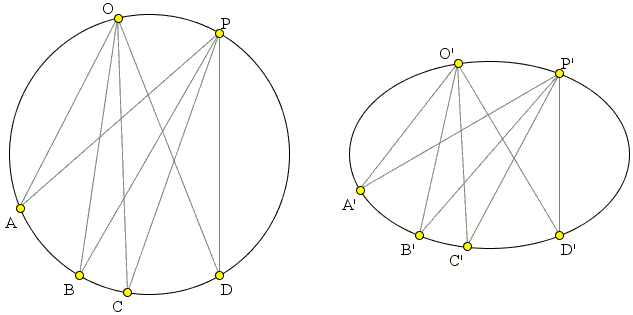
So let A, B, C, D, be four points (in this order in the diagram) on a circle with two additional points O and P on the arc AD not containing B and C. There are pairs of equal angles, e.g., ∠AOB = ∠APB, ∠BOC = ∠BPC, ∠COD = ∠CPD. This identities make pencils of lines at O and P congruent - the two can be superimposed on each other. It follows that the two pencils define exactly same cross-ratio: O(ABCD) = P(ABCD).

We see that for circles Chasles' theorem is an immediate consequence of the congruence of inscribed angles. However, the cross-ratio is preserved under projective mappings. The theorem is therefore true for all images of the circle, viz., all conic sections, as stated in the theorem. It is worth noting that the congruence of inscribed angles is not in general preserved by the projective mappings. In the right diagram, the six points are on an ellipse. ∠A'O'B' ≠ ∠A'P'B', etc. Nonetheless, O'(A'B'C'D') = P'(A'B'C'D').

References

R. Courant, H. Robbins, What is Mathematics?, Oxford University Press, 1996, pp. 202-203

Chasles' Theorem

Chasles' Theorem
Chasles' Theorem, a Simple Proof
Pascal's Theorem, Homogeneous Coordinates
Chasles' Theorem, a Proof
Projective Proof of Pascal's Theorem

72520375