Equilateral Triangle In a Pretty Diagram
Source
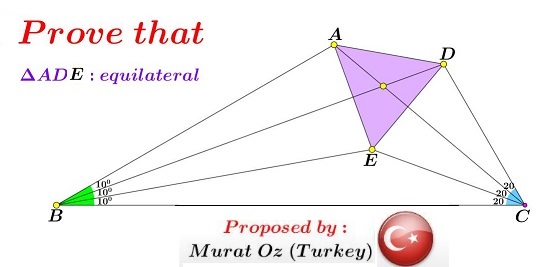
Problem
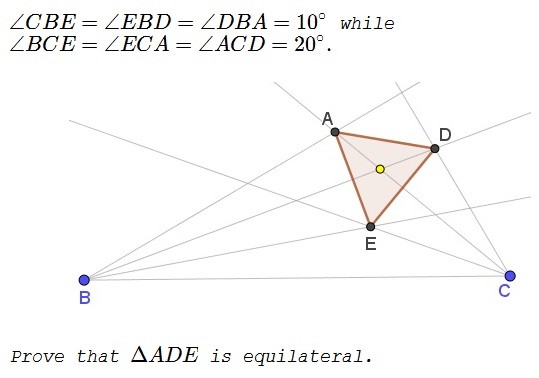
Solution 1
Let $I$ be the intersection of $BA$ and $CD,$ extended. Then in $\Delta BCI$ the given lines are trisectors of the angles at $B$ and $C.$ Add the trisectors at angle $A.$ Let $E,J,K$ be the intersections, as shown:
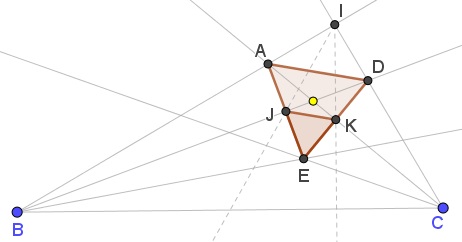
Then by Morley's Theorem $\Delta EJK$ is equilateral. In addition, $\displaystyle \angle CEK=\frac{\pi+\angle B}{3}=70^{\circ}$ and $\displaystyle \angle BEJ=\frac{\pi+\angle C}{3}=80^{\circ}.$ By simple angle chasing, in $\Delta CEK,$ $\angle CKE=90^{\circ}$ and, similarly, $\angle BJE=90^{\circ}.$
Let $D'=EK\cap CI$ and $A'=EJ\cap BI.$ Then, since $CK\perp D'E$ and $\angle CKE=\angle CKD',$ and also $\angle ECK=\angle CDK=02^{\circ},$ $\Delta CD'E$ is isosceles. In particular, $EK=KD'$ and $\angle CDE=\angle CEK=70^{\circ}.$ Similarly, $EJ=JA'$ and $\angle BA'E=\angle BEJ=80^{\circ}.$ Also, $A'D'\parallel JK,$ so that $\Delta A'D'E$ is equilateral.
We need to show that $A'=A$ and $D'=D.$
In equilateral $\Delta A'D'E,$ $A'J=JE$ so that $D'J\perp A'J$ but also $BJ\perp A'J,$ implying that $BJD'$ is a straight line and so is $CKA'.$ This exactly means that $D'=D$ and, similarly, $A'=A.$
Solution 2

In $\Delta HBC,$ $EB,EC$ are angle bisectors, implying that $HE$ is also an angle bisector. Thus,
$\angle BHC = 180^{\circ}-(20^{\circ}+40^{\circ})=120^{\circ},$so that $\angle BHE=\angle EHC=60^{\circ}.$ Also
$\angle AHB=\angle HCB+\angle HBC=40^{\circ}+20^{\circ}=60^{\circ}.$
It follows that $BAHE$ is a kite, so that $BH\perp AE$ and also $BH$ bisects $AE.$ In particular, $\Delta ADE$ is asosceles, i.e., $AD=ED.$
Similarly, $HDCE$ is a kite, implying $AD=AE.$ Thus $AD=ED=AE.$
Acknowledgment
The problem (by Murat Öz) has been posted at the Peru Geometrico facebook group by Miguel Ochoa Sanchez. They both have my sincere appreciation. Additional solutions can be found at the link.
Solution 2 is by David Nguyen.
Kadir Altinas has observed that the problem admits a generalization wherein the angles of $10^{\circ}$ are replaced by small $\alpha$ and those of $30^{\circ}$ by $30^{\circ}-\alpha.$ The proof remains the same. Kadir also noticed that there are non-symmetric configurations, e.g., $6-12-6, 12-18-18.$
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73517592
