Two Pencils of Parallel Lines
What Might This Be About?
Problem
Assume $E$ and $F$ are the midpoints of line segments $AB$ and $CD,$ respectively. Three parallel lines are drawn through $A,$ $E,$ and $B$ and another triple of parallel lines through $C,$ $F,$ and $D.$ The corresponding lines meet in $J,$ $K,$ and $L.$
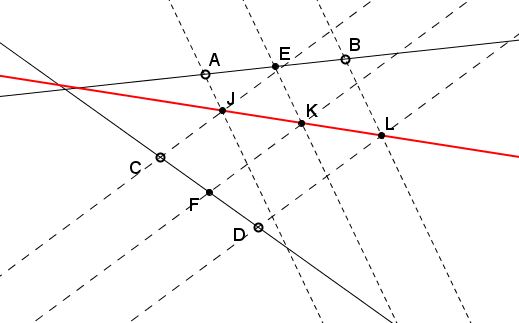
Prove that
$J,$ $K,$ and $L$ are collinear.
All such lines pass through a fixed point when the direction of one of the parallel triples changes.
Solution 1
I'll use complex variables. Let the first of the lines be defined by the parametric equation $f(t)=a+tb,$ the second by $g(t)=c+td,$ where $t$ is a real parameter, $a,b,c,d$ are complex numbers. I take $a$ to represent $A$ and $c$ to represent $C.$ Taking $b=B-A$ and $d=D-C$ allows to have parameter $t$ on both lines. The parallel lines are defined by $f_{t}(u)=a+tb+ue$ and $g_{t}(v)=c+td+vf,$ where are again $u$ and $v$ are real parameters while $e$ and $f$ are complex numbers.
Let's find the intersection of $f_{t}(u)$ and $g_{t}(v).$ The two lines intersect where their values coincide: $f_{t}(u)=g_{t}(v),$ and the task is to find where (or for what values of $u$ and $v)$ this happens. If two complex numbers are equal so are their conjugates, which I shall denote using the overbar: $\overline{z}.$ This gives two equations for the two unknowns, $u$ and $v$:
$\begin{align} f(t)+ue&=g(t)+vf\\ \overline{f(t)}+u\overline{e}&=\overline{g(t)}+v\overline{f}. \end{align}$
Since both $u$ and $v$ may be expected to be dependent on $t,$ I shall denote the solutions of these pair of equations as $u(t)$ and $v(t).$ Whichever way is chosen to solve that system, we obtain
$\begin{align}\displaystyle u(t)&=\frac{(g(t)-f(t))\overline{f}-(\overline{g(t)}-\overline{f(t)})f}{e\overline{f}-\overline{e}f}\\ v(t)&=-\frac{(g(t)-f(t))\overline{e}-(\overline{g(t)}-\overline{f(t)})e}{e\overline{f}-\overline{e}f}. \end{align}$
Note that, for any two complex numbers $x$ and $y,$ the expression $x\overline{y}-\overline{x}y$ is purely imaginary because
$\overline{x\overline{y}-\overline{x}y}=\overline{x}y-x\overline{y}=-(x\overline{y}-\overline{x}y).$
The ratio of two purely imaginary numbers is real, which shows that both $u(t)$ and $v(t)$ are real, as could have been expected.
From the expression for $u(t)$ and $v(t)$ one conclusion follows immediately: say, $f_{t}(u(t))$ which is the point of intersection of $f_{t}(u)$ and $g_{t}(v)$ is a linear function of $t,$ thus proving part 1. For part 2, let's find the value of $t$ for which $u(t)=0.$ Equating the numerator $(g(t)-f(t))\overline{f}-(\overline{g(t)}-\overline{f(t)})f$ to $0:$
$\begin{align} 0&=(g(t)-f(t))\overline{f}-(\overline{g(t)}-\overline{f(t)})f\\ &=[(c-a)\overline{f}-((\overline{c)}-\overline{a})f]+[(d-b)\overline{f}-(\overline{d}-\overline{b})f]t, \end{align}$
implying that $u(t)=0$ for
$\displaystyle t=-\frac{(c-a)\overline{f}-(\overline{c}-\overline{a})f}{(d-b)\overline{f}-(\overline{d}-\overline{b})f}, $
independent of $e!$ Let's denote that as $t_f:$ $u(t_{f})=0$ so that point $f(t_{f})=a+t_{f}b$ belongs 1) to $f(t)$ and 2) to any line of intersections of the two sets of parallel lines independent of the direction $e.$
(Compare this to a problem by V. Nikolin.)
Solution 2
Part 1 is the consequence of Thales' theorem and its converse. Consider two pairs of parallel lines: one through $A$ and $B,$ the other through $C$ and $D.$ These define points $J$ and $L$ and, therefore, the line $JL.$
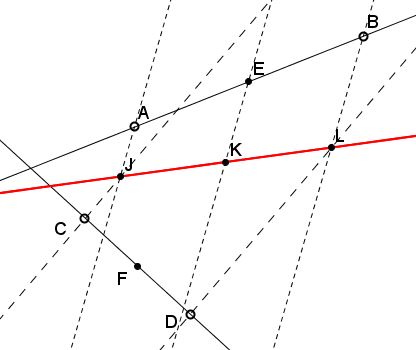
The line through $E$ parallel to the first two, meets $JL$ at $K$ such that, by Thales' theorem, $JK=KL.$ If we now join $K$ to $F$ - the midpoint of $CD$ - then by the converse of Thales' theorem $FK$ will be parallel to the second pair of lines. This proves Part 1.
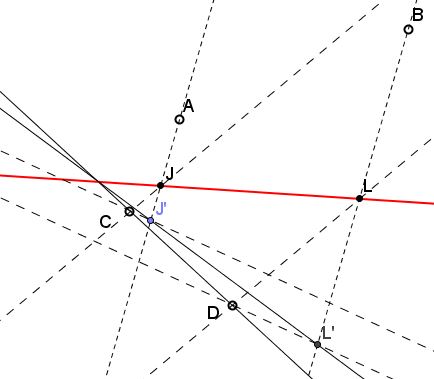
Fix parallels through $A$ and $B$ and consider two pairs of parallels through $C$ and $D.$ The first pair gives intersection points $J$ and $L,$ the second the intersections $J'$ and $L'.$ Triangles $CJJ'$ and $DLL'$ have pairwise parallel sides and are, therefore, homothetic. The three lines $JL,$ $J'L',$ and $CD$ all pass through the center of the homothety which, thus, lies on $CD.$ Fixing one direction and, say, points $J$ and $L$ and letting parallels through $C$ and $D$ change direction we see that all resulting lines $J'L'$ pass through the same point - the intersection of $CD$ and $JL.$
It could also be observed that the two triangles with pairwise parallel sides are perspective from a line - the line at infinity, in this case - and, therefore by Desargues' theorem, are also perspective from a point.
Solution 3
Fix a pair of parallel lines through $A$ and $.$ Let $C'$ and $D'$ be their intersection pointswith the line $CD.$ Then $(XCD)=(XJL)=(XC'D')$ where $(UVW)=UW/WV,$ counted with directed segments.
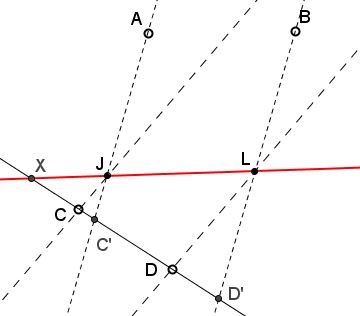
$C,$ $D,$ $C',$ $D'$ are fixed, and there is only one point $X$ on the line $CD$ that satisfies the equation: $XD/DC=XD'/D'C'$ or $(x-d)/(d-c)=(x-d')/(d'-c'),\space$ assuming $CD$ is linearly parametrized.
These are two linear functions on $CD$ in $x$ and, thus, the equation has only one solution. So, $C,$ $D,$ $C',$ $D'$ determine $X$ uniquely.
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page. The second solution is due to the efforts of Machó Bónis and Wojtek Wawrów. The third solution is due to Machó Bónis.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73577366
