Two Pairs of Parallel Lines in a Triangle

Hubert Shutrick came up (June 30, 2012) with the following generalization of a problem suggested by Vladimir Nikolin:

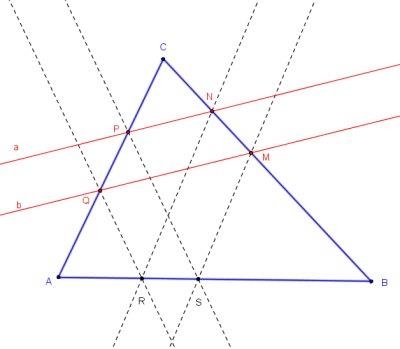
In a given ΔABC, points P, Q ∈ AC and M, N ∈ BC. (MQ and NP need not be parallel!) Construct (ruler-compass) points R, S on AB so that QR||PS and NR||MS.

Solution

In a given ΔABC, points P, Q ∈ AC and M, N ∈ BC. Construct (ruler-compass) points R, S on AB so that QR||PS and NR||MS.

Solution

Hubert's solution below is illustrated by the GeoGebra applet below (points A, B, C, P, Q, M, N are draggable):

Let N' be the point on AM such that QN'||PM, then NN' meets AB at R and the parallel line through M meets it at S.

Indeed, since MS||NR, triangles AMS and AN'R are similar, so that AR/AS = AN'/AM. Since PM||QN', triangles APM and AQN' are similar, so that AQ/AP = AN'/AM. It follows that AQ/AP = AR/AS, making triangles AQR and APS similar and lines QR and PS parallel.

After all, Hubert has been proved to be right: "Facile comme bonjour!" but one had to have this insight.