Three lines at 60 degres and Circumcenters

What Might This Be About?

Problem

Given three lines through points $A,$ $B,$ $C$ at $60^{\circ}$ to each other. The lines intersect at points $A',$ $B',$ $C'$ as shown in the diagram below.

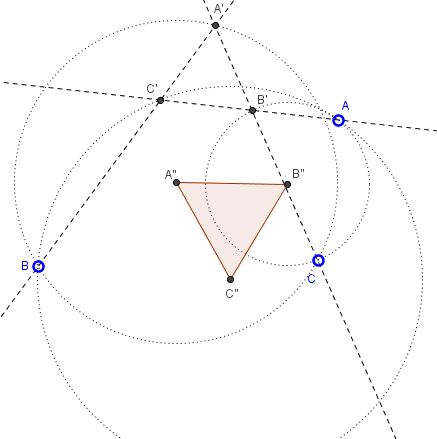
three lines at 60 degrees and circumcenters

Define $A'',$ $B'',$ $C''$ to be the circumcenters of triangles $A'BC,$ $AB'C,$ and $ABC',$ respectively. Then $\Delta A''B''C''$ is equilateral.

The problem could be reformulated in a somewhat mysterious manner:

Assume points $A,$ $B,$ $C$ are chosen randomly on the sides of an equilateral $\Delta A'B'C',$ such that $A$ lies on $B'C',$ etc. Define $A'',$ $B'',$ $C''$ to be the circumcenters of triangles $A'BC,$ $AB'C,$ and $ABC',$ respectively. Then $\Delta A''B''C''$ is equilateral.

Hint

The problem is very simple; just recollect the definition and the construction of the circumcenter.

Solution

First note that $\Delta A'B'C'$ is equilateral. Draw the six perpendicular bisectors that are required to form the circumcenters $A'',$ $B'',$ $C''.$ These are the bisectors of the segments $AB',$ $AC',$ $BA',$ $BC',$ $CA',$ $AB'.$

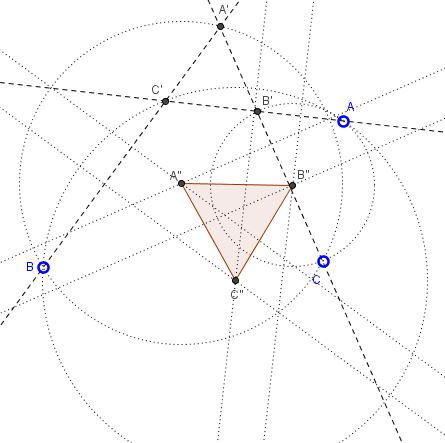
three lines at 60 degrees and circumcenters - solution

These lines form several equilateral triangles, and importantly are pairwise at the same distance. For example, the distance between the bisectors of the segments $AB'$ and $AC'$ is $B'C'/2.$ Similar claims hold for the other two pairs of bisectors. The distances between the bisectors equal half one of the sides of $\Delta A'B'C'.$

Since the latter is equlateral, the bisectors come in parallel pairs where the lines are at a fixed distance from each other.

Now the rest of the argument is based on the following diagram:

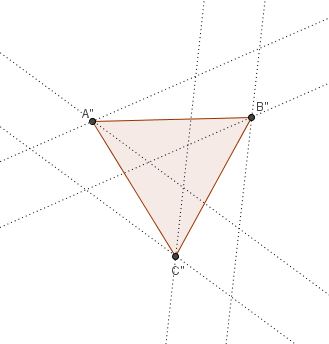
three lines at 60 degrees and circumcenters - solution, part 2

and is left to the reader, i.e., you.

Note

This is actually the configuration of Miquel's theorem for $\Delta A'B'C'.$ By the theorem, the three circles $(A''),$ $(B''),$ $(C'')$ are concurrent at a point. So what we have is this: the circumcenters of the three circles in Miquel's configuration of an equilateral triangle form another equilateral triangle. But then more can be said, viz., for any $\Delta A'B'C',$ and points $A,$ $B,$ $C,$ $\Delta A''B''C''$ is similar to $\Delta A'B'C'.$

Acknowledgement

This is a mistaken interpretation of the problem posted by Dao Thanh Oai at the CutTheKnotMath facebook page. This is delt with on a

separate page.

71946026