Miquel Circumcenters
What Might This Be About?
Problem
Points $A',$ $B',$ $C'$ are on the side lines of $\Delta ABC$ as shown in the diagram below.
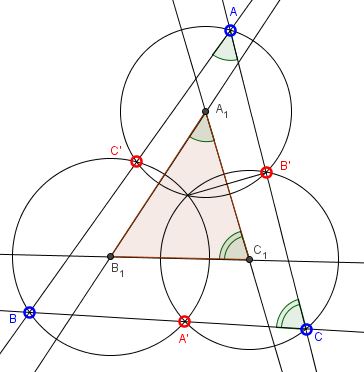
Define $A_1,$ $B_1,$ $C_1$ to be the circumcenters of triangles $AB'C',$ $A'BC',$ and $A'B'C,$ respectively. Then triangles $ABC$ and $A_1B_1C_1$ are similar.
Hint
The configuration is that of Miquel's theorem. The three circles concur at a point. This begs for the technique known as "chasing angles."
Solution
Note that the three circles meet at a point, call it $D.$ Join $A_1$ to $B',$ $C',$ and $D,$ and consider inscribed and central angles in circle $C(AB'C').$
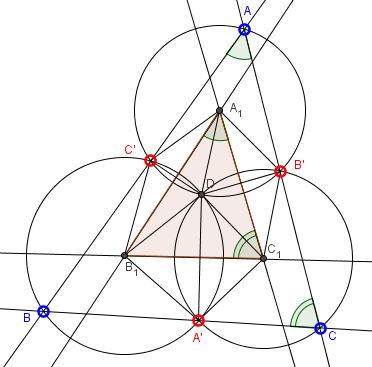
First of all, $\angle B'A_1C' =2\angle B'AC'.$ Second of all, $A_1B_1$ bisects $\angle C'A_1D,$ $A_1C_1$ bisects $\angle B'A_1D,$ implying that $2\angle B_1A_1C_1=\angle B'A_1C'.$ It follows that $\angle B_1A_1C_1=\angle BAC.$
The two remaining pairs of angles are treated similarly.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581672
