Equilateral Triangles Formed by Circumcenters

What Might This Be About?

Problem

Segments $AA',$ $BB',$ $CC'$ are equal in length and at $60^\circ$ to each other. The lines they are on intersect at points $A_1,$ $B_1,$ and $C_1,$ as shown below:

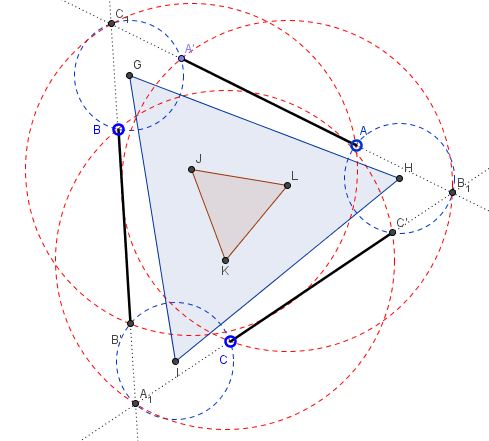
Equal segments at 60 degrees - problem

Prove that the circumcenters of triangles $AB_1C',$ $A'BC_1,$ $A_1B'C$ form an equilateral triangle, and so are the circumcenters of triangles $A'B_1C,$ $AB'C_1,$ $A_1BC'.$

Hint

The configuration in the problem is practically the same as that of Miquel's circumcenters. Here, too, we can detect three pairs of parallel lines with the same distance between the lines in a pair.

Solution

$\Delta A_1B_1C_1$ is equilateral.

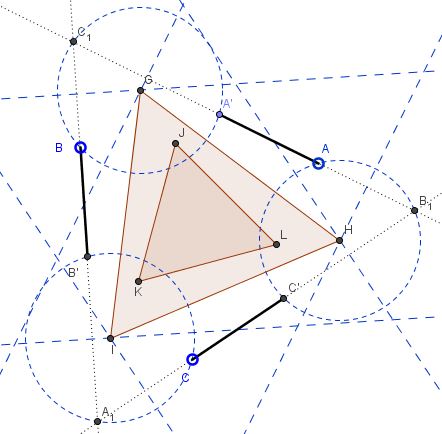
Equal segments at 60 degrees - solution

The distance between the perpendicular bisectors of $A'C_1$ and $AB_1$ equals $(B_1C_1 - AA')/2$ which is the same for the other two pairs of bisectors.

You are now asked to finish the proof.

Acknowledgment

The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.

70539321