Miquel's Point: What Is It?
A Mathematical Droodle
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Select a point on each side of a triangle or its extensions. By the Pivot Theorem, the three circles shown in the applet pass through the same point, the Miquel point of the three circles.
When the three selected points are collinear, the circumcircle of the given triangle also passes through the same point. The point is now called the Miquel point of the 4-line, i.e. of the four lines.
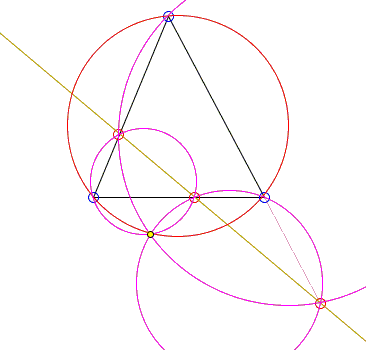
Following is the proof of that statement.
Given a 4-line, number the lines 1, 2, 3 and 4. There are four ways to take 3 lines at a time. Each gives us a triangle and its circumcircle. We are to prove that the four circles share a point.
Consider two triangles, say 123 and 124. Their circumcircles intersect at two points of which one does not belong to any of the given lines. Call it P. Consider the simsons of P with respect to the two triangles. One passes through the feet of the perpendiculars to the lines 1, 2 and 3. The other passes through the feet of perpendiculars to the lines 1, 2 and 4. The two simsons thus share two points, and therefore coincide.
This means that the feet of the perpendiculars from P to the sides of the triangles 134 and 234 all lie on the same line which then must be the simson of P with respect to triangles 134 and 234. From here, P lies on the circumcircles of both triangles 134 and 234. The four circumcircles intersect at P!
Now, what if you have a 5-line. There are five ways to pick a 4-line out of five lines. In each case there is a Miquel's point. Do you think they are strewn out randomly? If so, think again.
References
- R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995.
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73607172
