Pedal Triangles of Inverse Points
What is this about?
Problem
Given point $P$ in the plane of $\Delta ABC$ let $P'$ be the inverse of $P$ in the circumcircle $(ABC);$ let $EDF$ and $E'D'F'$ be the pedal triangles of $P$ and $P',$ respectively, relative to $\Delta ABC.$
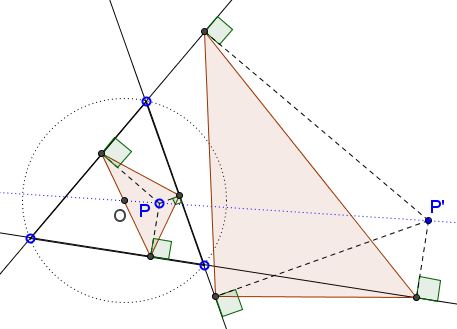
Prove that triangles $EDF$ and $E'D'F'$ are (inversely) similar.
Proof
Assume line $PP'$ that passes through the circumcenter $O$ crosses the circumcircle at points $S$ and $T,$ as shown, so that $ST$ is a diameter of $(O)=(ABC).$
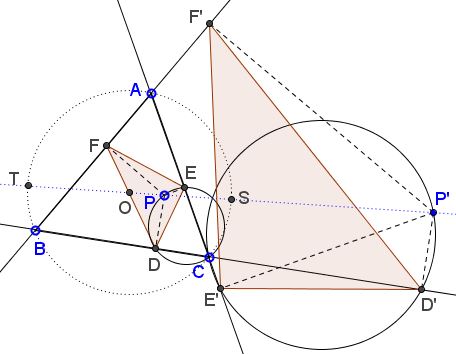
There are several ways to obtain the required result. The shortest is to observe that, say, circles $(CDPE)$ and $(CD'P'E')$ have the same inscribed angle at $C,$ implying that the central triangles in the two circles with bases $DE$ and $D'E'$ are similar so that the ratio $DE:D'E'$ equals the ratio of the two radii, or of the two diameters:
$\displaystyle\frac{DE}{D'E'}=\frac{CP}{CP'}.$
Now, it is known that the circle of inversion serves as an Apollonian circle for a pair of inverse points. In other words, the ratio $\displaystyle\frac{XP}{XP'}$ is the same for all points $X$ on $(ABC).$
In particular that means that
$\displaystyle\frac{AP}{AP'}=\frac{BP}{BP'}=\frac{CP}{CP'}=r,$
for some $r\gt 0.$ As we just saw, also $\displaystyle\frac{DE}{D'E'}=r.$ Similarly, $\displaystyle\frac{FE}{F'E'}=\frac{DF}{D'F'}=r,$ implying similarity of triangles $DEF$ and $D'E'F'.$ The two triangles have different orientations and are, therefore, inversely similar. Each is directly similar to the corresponding circumcevian triangle, making the latter two inversely similar. Since they are inscribed into the same circle, the two circumcevians are acually equal but have opposite orientations.
References
- N. Altshiller-Court, College Geometry, Dover, 1980, 172-174
- W. Gallatly, The Modern Geometry of the Triangle, Scholarly Publishing Office, University of Michigan Library (December 20, 2005), 22-23
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73572060
