Pedal Similarity
What Might This Be About?
Statement
Let $P$ be a point in the plane of $\Delta ABC;$ $A',B',C'$ the intersections of $AP,BP,CP$ with the circumcircle $(ABC).$ $\Delta DEF$ is the pedal triangle of $P$ relative to $\Delta ABC.$
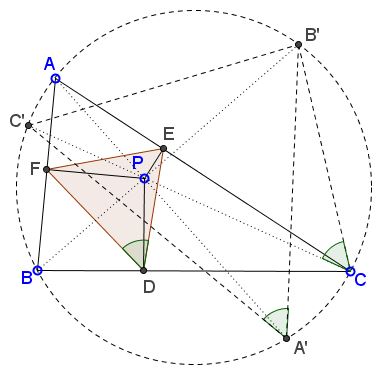
Triangles $DEF$ and $A'B'C'$ are similar.
Proof
Triangle $A'B'C'$ is known as the circumcevain triangle of point $P,$ and the property at hand has been established elsewhere by elegant and characteristic of the situation angle chasing. Below, I use another form of angle chasing with a reference to a different page.

In deriving the formula for $[\Delta DEF]$ we found that $\angle EDF=\angle ACB'.$ But, as two inscribed angles subtended by the same chord, $\angle B'CC'=\angle B'A'C'.$ By transitivity of equality $\angle EDF=\angle B'A'C'.$ Similarly, $\angle DEF=\angle A'B'C'$ and $\angle DFE=\angle A'C'B'.$
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581865
