Thales on Angle Bisectors
Source
The following problem has been posted by Miguel Ochoa Sanchez at the CutTheKnotMath facebook page. Leo Giugiuc posted a solution (Solution 2 below) by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc.
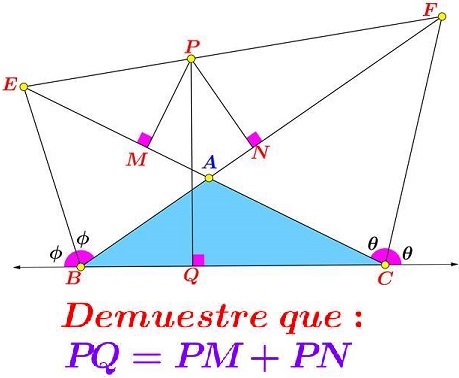
Problem
Let $BE$ and $CF$ be external angle bisectors in $\Delta ABC;$ $E$ is on $AC$ or its extension, $F$ is on $AB$ or its extension. From point $P$ on $EF$ perpendiculars $PM,$ $PN,$ $PQ$ are drawn to $AC,$ $AB,$ and $BC,$ respectively.
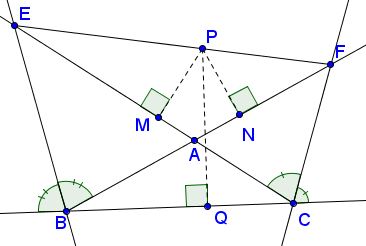
Prove that
$PM+PN=PQ.$
Solution 1
Let's first formulate simple affine lemma that is based on Thales' Theorem:
Lemma
Assume $A,X,B$ are collinear as are $A',X',B'.$ Suppose $AA'\parallel XX'\parallel BB'$ and $AX:XB=r:s.$
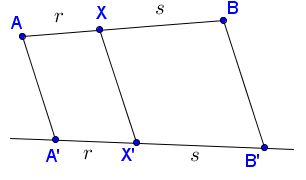
Then $\displaystyle XX'=\frac{s}{r+s}AA'+\frac{r}{r+s}BB'.$
To continue with the solution assume $EP:PF=r:s,$ $r+s=1,$ and consider two extreme positions of $P:$ one when $P=E,$ the other when $P=F.$ Indices $_e$ and $_f$ are added to distinguish between different endpoints $M,N,Q.$

Note that $M_e=E$ and $N_f=F,$ such that $EM_e=FN_f=0$ and, since $BE$ and $CF$ are angle bisectors, $EN_e=EQ_e$ and $FM_f=FQ_f.$ According to the lemma,
$PM=sEM_e+rFM_f=rFM_f,\\ PN=sEN_e+rFN_f=sEN_e,\\ PQ=sEQ_e+rFQ_f,$
so that
$\begin{align} PQ &= sEQ_e+rFQ_f\\ &= sEN_e+rFM_f\\ &= PM+PN. \end{align}$
Solution 2
Since $BC$ is the greatest side, we may choose $A(0,1)$, $B(-b,0)$ $C(c,0),$ where $b,c\gt 0.$ We'll find the locus of point $X(n,m)$ such that $d(X,AB)+d(X,A)=d(X,B)$ and $X$ is not in any open half-planes $(B,AC),$ $C,AB),$ or $(A,BC).$
Under our assumptions, $-m+bn-b\ge 0,$ $m+cn-c\ge 0,$ and $n\ge 0.$ We have $\displaystyle d(X,AB)=\frac{-m+bn-b}{\sqrt{b^2+1}},$ $\displaystyle d(X,AC)=\frac{m+cn-c}{\sqrt{c^2+1}},$ and $d(X,BC)=n.$ We thus seek $X$ for which $\displaystyle \frac{-m+bn-b}{\sqrt{b^2+1}}+\frac{m+cn-c}{\sqrt{c^2+1}}=n,$ implying that the sought locus is a straight line. By the external bisector theorem, $FA/FB=CA/CB,$ such that $F$ is defined by $\displaystyle\left(\frac{b\sqrt{c^2+1}}{b+c-\sqrt{c^2+1}},\frac{b+c}{b+c-\sqrt{c^2+1}}\right).$ By replacing we get immediately that $F\in l.$ Similarly, $E\in l.$ Hence, also $P\in EF.$ We are done.
Extra
It was observed by Dao Thanh Oai that the same arguments applies in the case of internal bisectors:
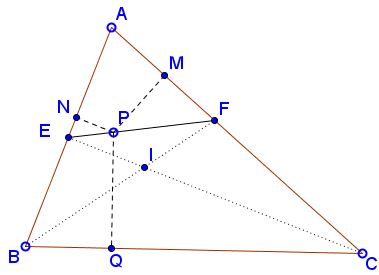
$PM+PN=PQ.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581151
