Bisectors And Proportions

Source

Leo Giugiuc has kindly posted at the CutTheKnotMath facebook page one of the problems from the 2015 Iberoamerican Mathematical Olympiad:

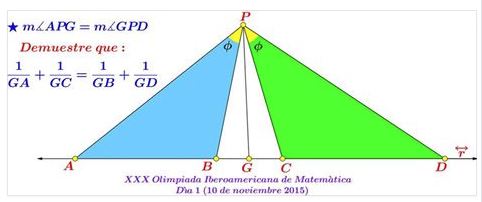
Bisectors And Proportions - source

Problem

Given $\Delta ADP$ and angle bisector $PG.$ Points $B$ and $C$ on $AD$ are such that $\angle APB=\angle CPD.$

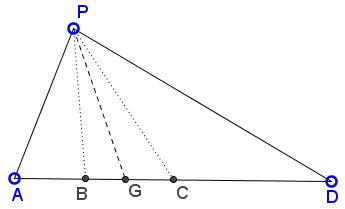
Bisectors And Proportions - problem

Prove that

$\displaystyle\frac{1}{GA}+\frac{1}{GC}=\frac{1}{GB}+\frac{1}{GD}.$

Solution 1

The solution depends on the following

Lemma

Let in $\Delta RST,$ $RU$ be a cevian through vertex $R.$ Introduce angles $\alpha = \angle SRU$ and $\beta = \angle URT.$

Then

$\displaystyle\frac{\sin (\alpha+\beta )}{RU} = \frac{\sin\alpha}{RT} + \frac{\sin\beta}{RS}.$

The lemma has been proved elsewhere.

Set up angles $\alpha$ and $\beta$ as below and apply Lemma to triangles $AGP$ and $DGP.$

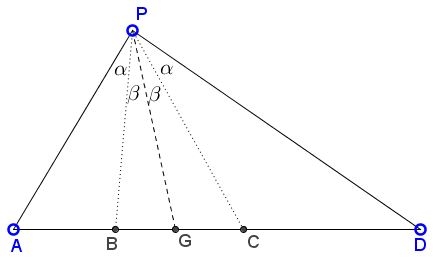
Bisectors And Proportions - solution

With $PB$ as a cevian in $\Delta AGP,$

$\displaystyle\frac{\sin (\alpha+\beta )}{PB} = \frac{\sin\beta}{PA} + \frac{\sin\alpha}{PG}.$

With $PC$ as a cevian in $\Delta DGP,$

$\displaystyle\frac{\sin (\alpha+\beta )}{PC} = \frac{\sin\beta}{PD} + \frac{\sin\alpha}{PG}.$

Subtracting one from the other we get

$\displaystyle\sin (\alpha+\beta )\left(\frac{1}{PB}-\frac{1}{PC}\right) = \sin\beta\left(\frac{1}{PA} - \frac{1}{PD}\right).$

Now, by the properties of angle bisectors in triangles $ADP$ and $BCG,$

$\displaystyle\frac{PA}{PD}=\frac{GA}{GD}$ and $\displaystyle\frac{PB}{PC}=\frac{GB}{GC}.$

It follows, for example, that

$\displaystyle\frac{GC}{PC}\sin (\alpha+\beta)\left(\frac{1}{GB}-\frac{1}{GC}\right)=\frac{GD}{PD}\sin \beta\left(\frac{1}{GA}-\frac{1}{GD}\right).$

The problem will be solved if we can establish

$\displaystyle\frac{GC}{PC}\sin (\alpha+\beta)=\frac{GD}{PD}\sin \beta.$

Set $\gamma =\angle DGP:$

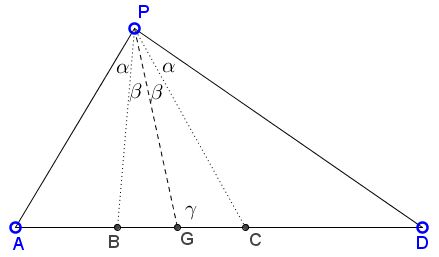
Bisectors And Proportions - solution, extra step

Apply the Law of Sines in triangles $DGP$ and $CGP:$

$\displaystyle\frac{GD}{\sin (\alpha+\beta)}=\frac{PD}{\sin\gamma}$ and $\displaystyle\frac{GC}{\sin \beta}=\frac{PC}{\sin\gamma}.$

By eliminating $\sin\gamma$ from the two we get just what is required.

Solution 2

This solution is due to Miguel Ochoa Sanchez; it depends on the following

Lemma

Let in $\Delta ABC,$ $AD$ be a cevian through vertex $A.$ Introduce angles $\alpha = \angle BAD$ and $\omega = \angle CAD;$ $s=AB,$ $p=BD,$ $r=CD,$ $q=AC.$

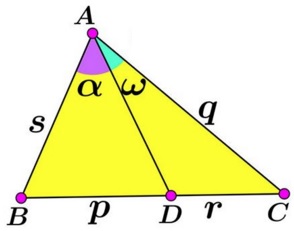
Bisectors And Proportions - solution, another extra step

Then

$\displaystyle\frac{\sin \alpha}{\sin\omega} = \frac{pq}{rs}.$

To prove the lemma, apply the Law of Sines to triangles $ABD$ and $ACD.$

Using the notations in the diagram below:

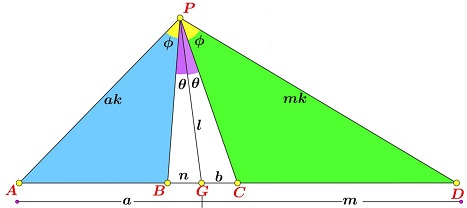
Bisectors And Proportions - solution 2

In $\Delta APG,$

$\displaystyle\frac{\sin\phi}{\sin\theta}=\frac{AB\cdot PG}{GB\cdot AP}=\frac{(a-n)l}{n(ak)}.$

In $\Delta DPG,$

$\displaystyle\frac{\sin\phi}{\sin\theta}=\frac{DC\cdot PG}{GC\cdot PD}=\frac{(m-b)l}{b(mk)}.$

Comparing the two gives

$\displaystyle\frac{(a-n)l}{n(ak)}=\frac{(m-b)l}{b(mk)}$

which is simplified to

$\displaystyle\frac{1}{n}-\frac{1}{a}=\frac{1}{b}-\frac{1}{m}.$

This is equivalent to the required identity.

Solution 3

Nevena Sybeva has posted the following solution that uses areas and the angle bisector theorem:

$\displaystyle\frac{[ABP]}{[CDP]}=\frac{PA\cdot PB\cdot\sin\phi}{PC\cdot PD\cdot\sin\phi}=\frac{PA}{PD}\cdot\frac{PB}{PC}=\frac{GA}{GD}\cdot\frac{GB}{GC}.$

On the other hand, we have

$\displaystyle\frac{[ABP]}{[CDP]}=\frac{AB}{CD}=\frac{GA-GB}{GD-GC}.$

Thus

$\displaystyle\frac{GA\cdot GB}{GD\cdot GC}=\frac{GA-GB}{GD-GC}.$

This is equivalent to

$\displaystyle\frac{1}{GA}+\frac{1}{GC}=\frac{1}{GB}+\frac{1}{GD}.$

Solution 4

Leo also posted a solution by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc.

71950161