Problem 4 from the IMO 2013 - Synthetic Solution

What Might This Be About?

Problem

Let $ABC$ be an acute triangle with orthocenter $H,$ and let $W$ be a point on the side $BC,$ lying strictly between $B$ and $C.$ The points $M and N$ are the feet of the altitudes from $B$ and $C,$ respectively. Denote by $\omega_1$ is the circumcircle of $BWN,$ and let $X$ be the point on $\omega_1$ such that $WX$ is a diameter of $\omega_1.$ Analogously, denote by $\omega_2$ the circumcircle of triangle $CWM,$ and let $Y$ be the point such that $WY$ is a diameter of $\omega_2.$

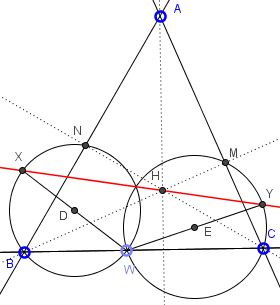
Prove that $X,$ $Y$ and $H$ are collinear.

Solution

Let $F$ be the other point of intersection of $\omega_1$ and $\omega_2.$ We know that $F$ lies on $XY.$

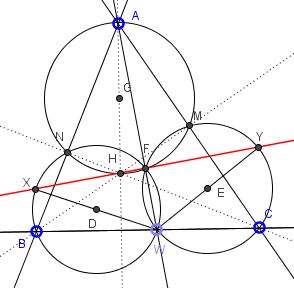
Problem 4 from the IMO 2013 - Synthetic Solution, extra point

Let $\omega$ be the third Miquel's circle, i.e., the circumcircle of $AMN.$ By Miquel's theorem, $F$ is on $\omega.$ $H$ is also on $\omega$ and what's more $AH$ is its diameter. This is because the two inscribed angles (one at $M,$ the other at $N$) are right, one pair of their sides intersects on $\omega$ (at $A$), so the other pair of their sides also intersects on $\omega.$ But these sides are formed by $BM$ and $CN$ that intersect at $H.$

Now, $\angle AFH=90^\circ,$ by Thales' Theorem. It follows that $AFW$ is a straight line. From $WF\perp XY$ together with $AF\perp FH$ we obtain that $H\in XY.$

Note: as in the case of the analytic solution, the requirementd that the triangel be acute and $W$ lie strictly between $B$ and $C$ are redundant.

Problem 4 from the IMO 2013 - Synthetic Solution, extra point

Suffice it to stipulate that $W$ does not coincide with either $B$ or $C$ and that the angles at $B$ and $C$ are not right.

71535950