Problem 4 from the IMO 2013
What Might This Be About?
Problem
Let $ABC$ be an acute triangle with orthocenter $H,$ and let $W$ be a point on the side $BC,$ lying strictly between $B$ and $C.$ The points $M and N$ are the feet of the altitudes from $B$ and $C,$ respectively. Denote by $\omega_1$ is the circumcircle of $BWN,$ and let $X$ be the point on $\omega_1$ such that $WX$ is a diameter of $\omega_1.$ Analogously, denote by $\omega_2$ the circumcircle of triangle $CWM,$ and let $Y$ be the point such that $WY$ is a diameter of $\omega_2.$
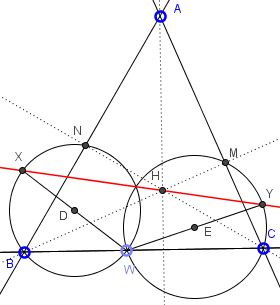
Prove that $X,$ $Y$ and $H$ are collinear.
Generalization
The solution below is by Leonard Giugiuc, Romania. As a matter of fact, Leonard proves a more general statement:
Let $ABC$ be a triangle with orthocenter $H;$ assume neither of the angles at $B$ or $C$ is right, and let $W$ be a point on the side line $BC$ different from either $B$ or $C.$ The points $M and N$ are the feet of the altitudes from $B$ and $C,$ respectively. Denote by $\omega_1$ is the circumcircle of $BWN,$ and let $X$ be the point on $\omega_1$ such that $WX$ is a diameter of $\omega_1.$ Analogously, denote by $\omega_2$ the circumcircle of triangle $CWM,$ and let $Y$ be the point such that $WY$ is a diameter of $\omega_2.$
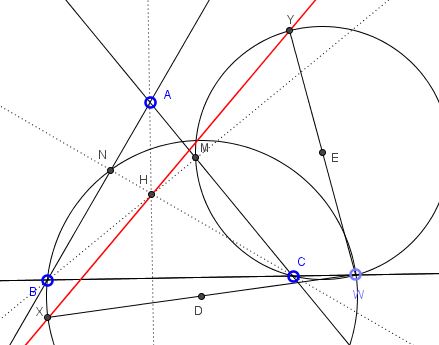
Prove that $X,$ $Y$ and $H$ are collinear.
Solution
Choose Cartesian coordinate system in which $A(0,2),$ $B(-2b,0),$ and $C(2c,0),$ $(b\ne 0\ne c).$ Then, $a=\cot B,$ $c=\cot C,$ and $H(0, 2bc).$ Let $W(2a,0),$ with $-b\ne a\ne c,$ and let $D$ and $E$ be the centers of $\omega_1$ and $\omega_2,$ respectively.
Then $D(a-b,y)$ and $E(a+c,z),$ for some $y$ and $z.$ $D$ is the midpoint of $WX$ and $E$ is the midpoint of $WY.$ Therefore, $X(-2b,2y)$ and $Y(2a,2z).$
The points $X,$ $Y,$ $H$ are collinear iff
$\left| \begin{array}{ccc} 0 & 2bc & 1 \\ -2b & 2y & 1 \\ 2c & 2z & 1 \end{array} \right|=0,$
i.e., when $bz+cy=bc(b+c).$
Let $N(2n,2q)$ be the feet the feet of the altitude from $C.$ Then, since the equation of $AB$ is $-x+by=2b,$ the equation of $CN$ is $\displaystyle\frac{x-2c}{-1}=\frac{y}{b}.$ Solving for $x$ and $y$ leads to $\displaystyle n=\frac{b(bc-1)}{1+b^2}$ and $\displaystyle q=\frac{b(b+c)}{1+b^2}.$
Further, $DN=DW$ implies
$(a+b)^{2}+y^{2}=(a-b-2n)^{2}+(y-2q)^{2}$
from which $\displaystyle y=\frac{n^2+q^2+nb}{q}-\frac{a(n+b}{q}.$ Substituting the values of $n$ and $q$ gives $y=bc-ab.$ Similarly, $z=bc+ab$ such that, indeed, $bz+cy=bc(b+c).$
Note: there is another, synthetic solution.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73571926
