Squares on Sides of a Parallelogram
What is this about?
Problem
Let similarly oriented squares $ABGH,\;$ $BCIJ,\;$ $CDKL,\;$ and $ADEF\;$ be erected on the sides of a parallelogram $ABCD.$ Assume $U,V,W,Z\;$ are the midpoints of segments $FH,\;$ $GJ,\;$ $IL,\;$ and $KE,\;$ respectively.
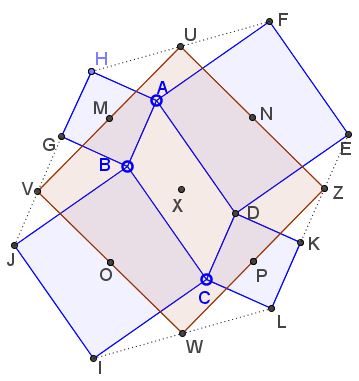
Prove that the quadrilateral $UVWZ\;$ is a square.
Proof 1
Denote the centers of the squares $ABGH,\;$ $BCIJ,\;$ $CDKL,\;$ and $ADEF\;$ as $M,\;$ $N,\;$ $P,\;$ and $O,\;$ respectively. Let $X\;$ be the intersection of the diagonals of $ABCD.\;$
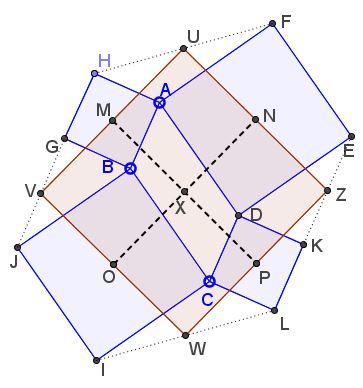
According to the Finsler-Hadwiger theorem, the quadrilaterals $XNUM,\;$ $XMVO,\;$ $XOWP,\;$ and $XPZN\;$ are all squares, directly implying that $UVWZ\;$ is also a square.
Proof 2
We'll use complex numbers: assume $X\;$ is the center $0,\;$ $A=a,\;$ $B=b,\;$ making $C=-a\;$ and $D=-b.$
Then, e.g., $F=a+i(-b-a)$ and $H=a-i(b-a)\;$ so that $\displaystyle U=\frac{F+H}{2}=a-ib.\;$ Similarly, $V=b+ia\;$ and $W=-U=-a+ib.$ It follows that $W-V=-(a+b)-i(a-b)\;$ and $U-V=(a-b)-i(a+b),\;$ implying $U-V=i(W-V)\;$ which exactly means that $\Delta UVW\;$ is right (at $V$) isosceles triangle. So are the triangles $VWZ,\;$ $WZU,\;$ and $ZUV,\;$ implying that $UVWZ\;$ is indeed a square.
Proof 3
In a more general problem where $ABCD\;$ is an arbitrary quadrilateral, $UW=VZ$ and $UW\perp VZ.$
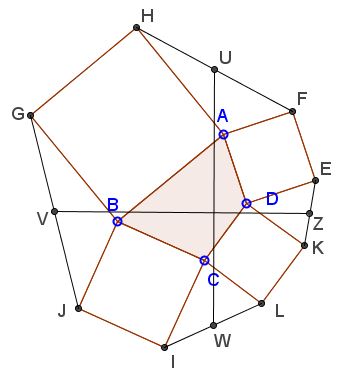
When $ABCD\;$ is a parallelogram, the configuration enjoys central symmetry; so both $UW\;$ and $VZ\;$ path through the center $X\;$ of the parallelogram and are divided by $X\;$ in half, exactly implying that they are the diagonals of a square.
Proof 4
Add a few lines to the configuration as shown below:
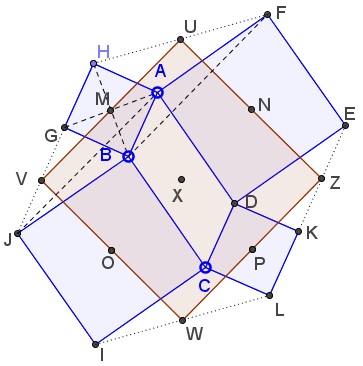
Observe that, by the construction, $MV\;$ is a midline in $\Delta AHJ,\;$ implying that $VM\parallel AJ\;$ and $VM=\frac{1}{2}AJ.\;$ Similarly $MU\parallel BF\;$ and $MU=\frac{1}{2}BF.\;$ Further, triangles $ABJ\;$ and $BAF\;$ are obtained from each other by the reflection in the midpoint of $AB,\;$ so that $AJ\parallel BF\;$ and $AJ=BF.\;$ From here, $M\;$ is the midpoint of $UV.\;$ Similarly, $N\;$ is the midpoint of $UZ\;$ and, in particular, $NU=\frac{1}{2}DH.\;$ But, as we know from Vecten's configuration, $DH=BF\;$ so that $UV=UZ,\;$ and, in the very least, $UVWZ\;$ is a rhombus.
The midpoints of the sides of a rhombus form a rectangle which becomes a square when the rhombus happens to be a square. This is so in our case as a consequence of Thébault's first problem which shows that $MNPO\;$ is a square, thus so is $UVWZ.$
Proofs 5 and 6
These are in a separate file in the Microsoft's docx format.
Proof 7
There is a one line proof based on the theory of the spectral decomposition of planar quadrilaterals.
Acknowledgment
The problem is a discovery of a mathematics teacher from Russia Galina Gavrilenko. Proof 4 was suggested by Augustini Moraru. Proofs 5 and 6 are the original proofs by Galina. Proof 7 is by Grégoire Nicollier.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73571709
