Squares on Sides of a Quadrilateral II
What is this about?
Problem
Let similarly oriented squares $ABGH,\;$ $BCIJ,\;$ $CDKL,\;$ and $ADEF\;$ be erected on the sides of a quadrilateral $ABCD.$ Assume $U,V,W,Z\;$ are the midpoints of segments $FH,\;$ $GJ,\;$ $IL,\;$ and $KE,\;$ respectively.
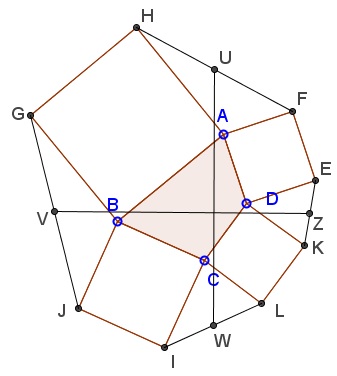
Then $UW=VZ\;$ and $UW\perp VZ,\;$ similar to the Van Aubel's Theorem.
Proof 1
We'll think of points as complex numbers. Then $F=A+i(D-A),\;$ $H=A-i(B-A),\;$ so that $\displaystyle U=\frac{2A+i(D-B)}{2}.\qquad$ Similarly, $\displaystyle V=\frac{2B+i(A-C)}{2},\;$ $\displaystyle W=\frac{2C+i(B-D)}{2},\;$ $\displaystyle Z=\frac{2D+i(C-A)}{2}.$
It follows that $\displaystyle W-U=\frac{2(C-A)+2i(B-D)}{2}=(C-A)+i(B-D).\qquad$ Similarly $Z-V=(D-B)+i(C-A).\;$ Clearly $Z-V=i(W-U),\;$ which proves the claim.
Proofs 2
There is a one line proof based on the theory of the spectral decomposition of planar quadrilaterals.
Extra
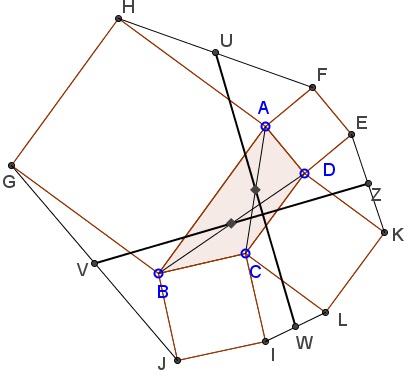
The configuration at hand has additional features. For examlpe, $UW\;$ and $AC\;$ share a midpoint, as are $VZ\;$ and $BD.$
Acknowledgment
The statement arose in one of the proofs of a discovery by a mathematics teacher from Russia Galina Gavrilenko. Proof 2 is by Grégoire Nicollier.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73569737
