Finding the Circumradius of the Excentral Triangle
Problem
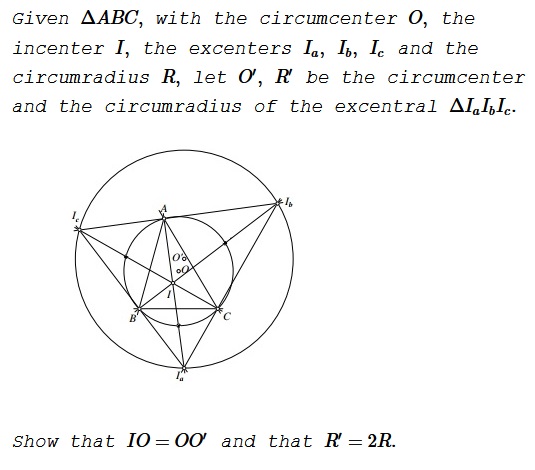
Solution 1
We are going to use a beautiful property that is interesting in itself: The midpoint $D$ of the arc $\overset{\frown}{a}$ in the circumcircle $(ABC)$ that does not contains $A$ is the center of a circle that passes through the points $B,$ $C,$ $I$ and $Ia.$ A similar observation applies to the midpoints $E$ and $F$ of the arcs $\overset{\frown}{CA}$ and $\overset{\frown}{AB}$ that are opposite vertices $B$ and $C,$ respectively: the circumcircle $(AICI_b)$ is centered at $E$ whereas $(AIBI_c)$ is centered at $F.$
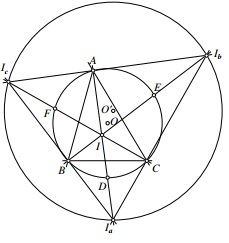
In other words, the segments $II_a,$ $II_b,$ $II_c$ are each halved by the circumcircle $(ABC),$ implying that the circumcircle $(I_aI_bI_c)$ is homothetic with the circumcircle $(ABC)$ from the incenter $I,$ the factor of homothety being $2.$ Thus $R'=2R$ and $IO'=2IO,$ i.e., $IO=OO'.$
Solution 2
By chasing angles, we find the following duality: $ABC$ is the orthic triangle of the acute $I_aI_bI_c.$ So $I$ is the othocenter of $I_aI_bI_c$ and $O$ is the $NPC$ center of the same triangle. We are done.
Acknowledgment
The above proof is by Francisco Javier García Capitán to a problem that is usually solved with a reference to the nine-point circle. Solution 2 is by Leo Giugiuc.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574466
