A Theorem of M. Mansion
What Is This About?
Problem
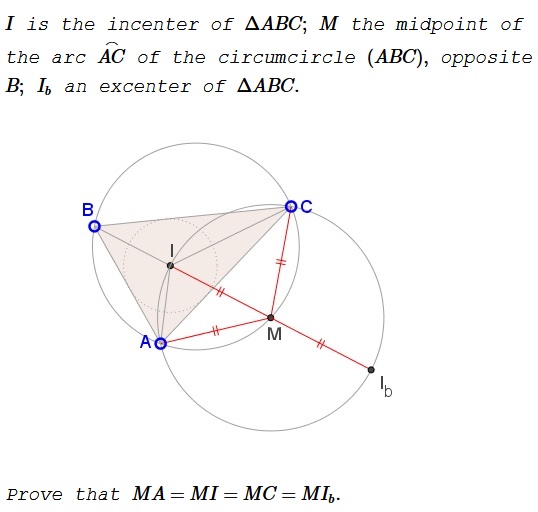
Solution
Elsewhere it was shown that $MA=MI=MC$ so that $M$ is the circumcenter of $\Delta ACI.$ Since $I$ and $M$ lie on the internal bisector of $\angle ABC$ that also passes through the excenter $I_b,$ suffice it to show that $I_b$ lies on $(M)=(ACI).$
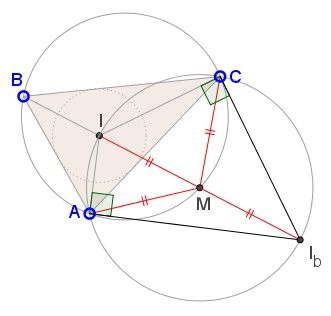
The excenter $I_b$ is also the intersection of the external angle bisectors at $A$ and $C,$ that are perpendicular to the respective internal angle bisectors. This makes the quadrilateral $AICI_b$ cyclic, placing $I_b$ on the circle $ACI.$
Reformulation
Let $I$ be the incenter, $I_b$ an excenter of $\Delta ABC.$ Then the circumcrcle $(ABC)$ cuts the segment $II_b$ in half.
Acknowledgment
I am grateful to Konstantin Knop for pointing out this theorem and the attribution. The only online source for the statement is the Russian version of the wikipedia.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73608120
