Concurrent Cevians and a Conic through Their Feet
What is this about?
Problem
In $\Delta ABC$ cevians $AD$, $BE$, and $CF$ meet at point $W$.
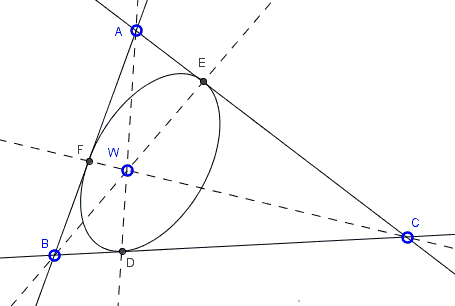
Prove that there is a conic tangent to $BC$ at $D,$ $AC$ at $E,$ and $AB$ at $F.$
Hint
I know of at least two ways to prove the statement: 1) using homogeneous coordinates (which I do below); 2) using pencils of conics (has been done by Hubert Shutrick elsewhere.
Solution
There are two basic references at the site that introduce the tools I'll use below:
As an example, homogeneous coordinates was useful in establishing Pascal's and Chasles' theorems.
I find it convenient here to denote the point with (homogeneous) coordinates $\alpha,$ $\beta,$ $\gamma$ as $\alpha :\beta :\gamma.$
So let there be a point, say $W(\alpha :\beta :\gamma )$ in the plane of $\Delta ABC.$ With homogeneous barycentric coordinates we have the following diagram:
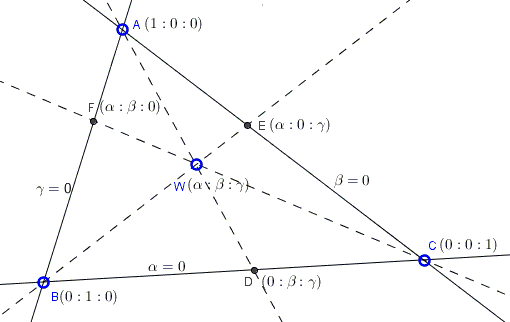
A conic in homogeneous coordinates $x:y:z$ has an equation of the form:
$f(x:y:z) = ax^{2}+by^{2}+cz^{2}+2dyz+2exz+2fxy=0$
The task is to determine coefficients $a,b,c,d,e,f$ for which the conic is tangent at points $D,E,F$ to the side lines of $\Delta ABC.$
In order for it to pass through point $D(0:\beta :\gamma)$ we need:
$f(0:\beta :\gamma) = b\beta^{2}+c\gamma^{2}+2d\beta\gamma=0,$
from which $\displaystyle d=-\frac{b\beta^{2}+c\gamma^{2}}{2\beta\gamma}.$ Similarly, for points $E$ and $F$ to belong to the conic, one needs
$\displaystyle e=-\frac{a\alpha^{2}+c\gamma^{2}}{2\alpha\gamma}$ and
$\displaystyle f=-\frac{b\alpha^{2}+c\beta^{2}}{2\alpha\beta}.$
In general, if point $x':y':z'$ lies on conic $f(x:y:z) = 0$ the tangent to the conic through $x':y':z'$ is given by the equation
$(ax'+ez'+fy')x+(by'+dz'+fx')y+(cz'+dy'+ex')z=0.$
At point $D(0:\beta :\gamma)$ we obtain
$(e\gamma +f\beta)x+(b\beta+d\gamma)y+(c\gamma+d\beta)z=0.$
For the equation to be equivalent to $\alpha=0$ we should only find $b$ and $c$ for which $(b\beta+d\gamma)=(c\gamma+d\beta)=0.$ Similarly, for the other two sides and the two points. In all, we obtain three analogous equations (do not forget that $d,e,f$ have been expressed in terms of $a,b,c).$ For example,
$\displaystyle b\beta+d\gamma=b\beta-\frac{b\beta^{2}+c\gamma^{2}}{2\beta}=\frac{b\beta^{2}-c\gamma^{2}}{2\beta},$
which vanishes if $b:c=\gamma^{2}:\beta^{2}.$ Similarly, we also need
$a:b=\beta^{2}:\alpha^{2}$ and
$c:a=\alpha^{2}:\gamma^{2}.$
Of the three equations only two are independent. It is easy to satisfy all three by choosing
$a:b:c=\beta^{2}\gamma^{2}:\alpha^{2}\gamma^{2}:\alpha^{2}\beta^{2}.$
This is actually a unique choice that gives a unique conic through points $D,E,F$ at which it is tangent to the side lines $BC,$ $AC,$ and $AB,$ respectively.
Acknowledgment
This problem generalizes the previously considered case where points $D,E,F$ were the midpoints of the sides of $\Delta ABC.$ The latter extends to prove the existence of an ellipse crossing the side lines around the midpoints. A similar extension, as was demonstrated by Hubert Shutrick, holds in the more general case of concurrent cevians.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73576504
