Two Conics, Pascal, Chasles, and Cross-Ratio
What is this about?
Problem
I use notations from a related problem; as stand alone they may appear somewhat weird.
Assume points $A_b,$ $A_c,$ $B_c,$ $B_a,$ $C_a,$ $C_b$ lie on a conic in such a manner that segments $A_{b}A_{c},$ $B_{a}B_{c},$ $C_{a}C_{b}$ are concurrent. Extend the sides of the hexagon to meet in points $A,$ $B,$ $C,$ $A_{a},$ $B_{b},$ $C_{c},$ as shown:
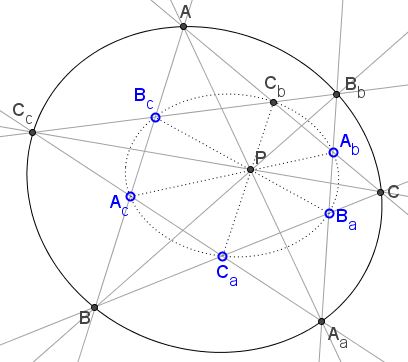
Then points $A,$ $B,$ $C,$ $A_{a},$ $B_{b},$ $C_{c}$ lie on a conic.
Proof 1
From Brianchon theorem we get there exist a conic inscribed hexagon $B_{c}C_{b}A_{b}B_{a}C_{a}A_{c},$ so $A(C_{c},B_{b};B_{c},C_{b})=A_{a}(C_{a},B_{a};B,C),$ i.e., $A,$ $A_{a},$ $C_{c},$ $B_{b},$ $B,$ $C$ lie on a conic.
Proof 2
The hexagon $A_{c}A_{b}B_{a}C_{a}C_{b}B_{c}$ has $BPB_{b}$ as the Pascal line, for $B=A_{c}B_{c}\cap B_{a}C_{a},$ $P=A_{c}A_{b}\cap C_{a}C_{b},$ and $B_{b}=A_{b}B_{a}\cap C_{b}B_{c}:$
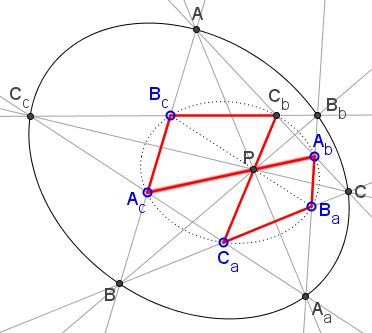
Similarly, $APA_{a}$ and $CPC_{c}$ are the Pascal lines of the other two hexagons - $B_{c}A_{c}C_{a}C_{b}A_{b}B_{a}$ and $A_{c}C_{a}B_{a}B_{c}C_{b}A_{b},$ respectively, - obtained from $B_{c}C_{b}A_{b}B_{a}C_{a}A_{c}$ by reordering the vertices.
The pencil of lines $P(C_{b}B_{c}C_{b}B_{b})$ is the same as $P(CB_{a}C_{a}B),$ implying the equality of cross-ratios $(C_{c},B_{b};B_{c},C_{b})=(C,B;B_{a},C_{a}),$ or $A(C_{c},B_{b};B_{c},C_{b})=A_{a}(C,B;B_{a},C_{a}).$ Further:
$\begin{align} A_{a}(C,B;B_{b},C_{c}) &= A_{a}(C,B;B_{a},C_{a})\\ &= A(C_{c},B_{b};B_{c},C_{b})\\ &= A(C_{c},B_{b};B,C)\\ &= A(C,B;B_{b},C_{c}), \end{align}$
where at the last step we used the well known dependency of the cross ratio on the order of the four points involved. Via Chasles' theorem $A_{a}(C,B;B_{b},C_{c})=A(C,B;B_{b},C_{c})$ leads to the required assertion that the six points $A_{a},C,B,B_{b},C_{c},A$ lie on a conic. (The last step may be seen as an elucidation of the last step of Proof 1.)
Acknowledgment
This is a slight modification of the problem posted by Tran Quang Hung at the CutTheKnotMath facebook page. The first solution is by Telv Cohl; Hubert Shutrick was instrumental in obtaining the second proof. He also observed that the statement admits a generalization.
![]()
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73583720
