A Conic in a Triangle
What is this about?
Problem
Let $P$ be a point in the plane of $\Delta ABC.$ Three lines through $P$ parallel to the sides of the triangle meet the sides at points $A_b,$ $A_c,$ $B_c,$ $B_a,$ $C_a,$ $C_b,$ as shown:
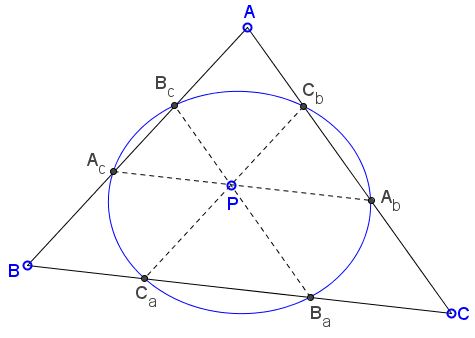
Then $A_b,$ $A_c,$ $B_c,$ $B_a,$ $C_a,$ $C_b$ lie on a conic.
Proof 1
Since $A_{b}A_{c}\parallel BC,$ Thales' theorem shows that
$ \displaystyle\frac{AA_{b}}{CA_{b}}=\frac{AA_{c}}{BA_{c}},\\ \displaystyle\frac{BB_{c}}{AB_{c}}=\frac{BB_{a}}{CB_{a}},\\ \displaystyle\frac{CC_{a}}{BC_{a}}=\frac{CC_{b}}{AC_{b}}. $
Taking the product yields
$\displaystyle\bigg(\frac{AB_{c}}{BB_{c}}\cdot\frac{AA_{c}}{BA_{c}}\bigg)\cdot\bigg(\frac{BC_{a}}{CC_{a}}\cdot\frac{BB_{a}}{CB_{a}}\bigg)\cdot\bigg(\frac{CA_{b}}{AA_{b}}\cdot\frac{CC_{b}}{AC_{b}}\bigg)=1.$
We only need to evoke Carnot's theorem for conics to conclude the proof.
Proof 2
Assume in homogeneous coordinates $A = (1, 0, 0),$ $B = (0, 1, 0),$ $C = (0, 0, 1),$ $P = (a,b,c),$ and the line at infinity given by $x+y+z=0.$ Then, for example, $AB,$ having equation $z=0,$ intersects the line at infinity at point $(1,-1,0)$ and the same is true for the line through $P(a,b,c)$ parellel to $AB.$ This line then meets $BC$ in $(a,b,c)-a(1,-1,0)=(0,a+b,c).$ This is point $C_a$ in the diagram: $C_{a}=(0,a+b,c).$
Similarly, $B_{a} = (0, b, a+c),$ $A_{c} = (a, b+c, 0),$ $B_{c} = (a+c, b, 0),$ $A_{b} = (a, 0, b+c)$ and $C_{b} = (a+b, 0, c).$ To test that they are on a conic, the obvious way is to use Pascal's theorem. Line $B_{a}C_{a}$ has the equation $a=0;$ line $B_{c}C_{b}$ $tB_{c}+sC_{b}=0.$ The two intersect when, say, $t=-(a+b),$ $s=(a+c),$ implying that the point of intersection is $(0, b(a+b), -c(a+c)).$ The other two intersections are $(a(a+b), 0, -c(b+c))$ and $(a(a+c), -b(b+c), 0).$ We need to write a determinant to verify that the three points are collinear:
$\begin{vmatrix} 0 & b(a+b) & -c(a+c)\\ a(a+b) & 0 & -c(b+c)\\ a(a+c) & -b(b+c) & 0 \end{vmatrix}= abc\begin{vmatrix} 0 & (a+b) & -(a+c)\\ (a+b) & 0 & -(b+c)\\ (a+c) & -(b+c) & 0 \end{vmatrix}$
The right determinant vanishes as the difference of two terms equal to $(a+b)(b+c)(a+c).$ This confirms that the three points are collinear and that $A_b,$ $A_c,$ $B_c,$ $B_a,$ $C_a,$ $C_b$ indeed lie on a conic.
Note: Hubert Shutrick wrote a clarification for the proof.
Proof 3
The opposite side of the hexagon $C_{a}B_{a}B_{c}A_{c}A_{b}C_{b},$ being parallel, meet on the line at infinity so Pascal's theorem gives that the vertices lie on a conic.
Note that this proof does not require the three lines through $P$ to be parallel to the sides of $\Delta ABC.$
Acknowledgment
The problem has been posted by Tran Quang Hung at the CutTheKnotMath facebook page. The first solution is by Telv Cohl, the second and third by Hubert Shutrick.
![]()
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73559188
