Beyond Viviani
Source
The problem below has been stated by Miguel Ochoa Sanchez:
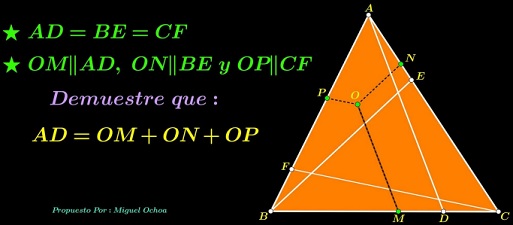
Problem
Cevians $AD,$ $BE,$ $CF$ in $\Delta ABC$ are equal. Points $M,N,P$ are on $BC,AC,AB,$ respectively, such that $OM\parallel AD,$ $ON\parallel BE,$ and $OP\parallel CF.$
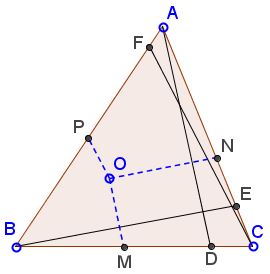
Prove that $OM+ON+OP=AD.$
Lemma
Let $O$ be a point within $\Delta ABC$ and $A'$ the intersection of $AO$ with $BC.$ Then, if $[X]$ denotes the area of shape $X,$
$\displaystyle\frac{[\Delta BOC]}{[\Delta BAC]}=\frac{OA'}{AA'}.$
Indeed, the areas at hand relate as their altitudes to $BC$ and these are proportional to $AA'$ and $OA'.$
Proof
Let denote $AD = BE = CF = s$ and $[OBC] = x$, $[OCA] = y,$ $[OAB] = z;$ we also denote $U = AO\cap BC.$ By the lemma above, $\displaystyle\frac{OU}{UA}=\frac{x}{x+y+z}.$
By Thales' theorem in $\Delta UAD,$ with $OM\parallel AD,$
$\displaystyle\frac{OU}{UA}=\frac{OM}{AD},$ i.e., $\displaystyle OM=\frac{sx}{x+y+z}.$
By analogy, $\displaystyle ON=\frac{sy}{x+y+z}$ and $\displaystyle OP=\frac{sz}{x+y+z}.$ Adding the three up completes the proof.
Acknowledgment
The original statement and the proof have been emailed to me by Leo Giugiuc with credits to Miguel Ochoa Sanchez. I have initially misunderstood the statement due to the triangle $ABC$ in Sanchez's diagram appearing to be equilateral. This led to the Slanted Viviani page which might be of interested in itself but does not reflect on a much deeper statement by Miguel Ochoa Sanchez. I humbly offer my apologies to both Miguel Ochoa Sanchez and Leo Giugiuc. My sincere gratitude goes to Grégoire Nicollier for drawing my attention to the original problem.
However, observe that the PWW of the Slanted Viviani case works for the more general problem of congruent cevians as long as the extra lines drawn are parallel to the sides of $ABC.$ The cevians in the small triangles are naturally drawn parallel to the given ones so that the congruence of the cevians is inherited by the small triangles.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579929
