Angles in a Triangle: an Exercise
Source
The following problem has been posted by Leo Giugiuc (Romania) at the CutTheKnotMath facebook page in the name of Miguel Ochoa Sanchez (Peru) who credited it to Kadir Altintas (Turkey). Leo also posted a solution (Solution 2 below) by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc.
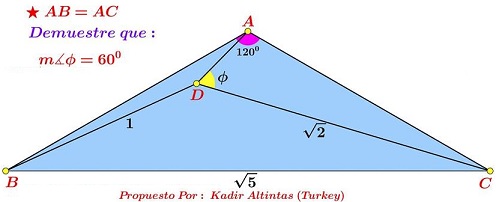
Problem
In $\Delta ABC;$ $AB=AC,$ $\angle BAC=120^{\circ},$ and $BC=\sqrt{5}.$ $D$ is a point inside $\Delta ABC$ such that $BD=1$ and $CD=\sqrt{2}.$
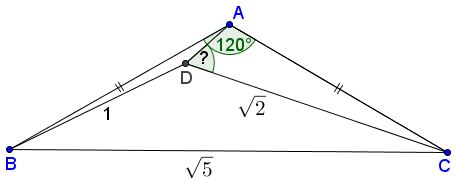
Prove that $\angle ADC=60^{\circ}.$
Solution 1
Rotate the diagram $120^{\circ}$ counterclockwise around $A:$ $B$ goes to $C,$ $C$ to $C',$ and $D$ to $D'.$
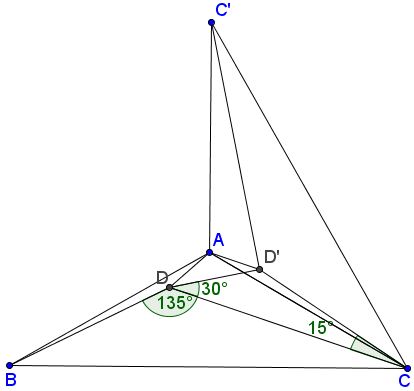
By the Law of Cosines in $\Delta BCD,$
$5=1-2\sqrt{2}\cos\angle BDC+2,$
such that $\displaystyle\cos\angle BDC = -\frac{\sqrt{2}}{2},$ giving $\angle BDC=135^{\circ}.$
We thus have $\angle CBD + \angle BCD = 45^{\circ},$ $\angle C'CD'=\angle CBD,$ $\angle BCC'=60^{\circ},$ leading to $\angle DCD'=15^{\circ}.$
$\displaystyle\sin 15^{\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}$ and $\displaystyle\cos 15^{\circ}=\frac{\sqrt{6}+\sqrt{2}}{4}.$
Since $CD'=BD=1,$ we can employ the Law of Cosines in $\Delta DCD'$ to find $DD':$
$\displaystyle (DD')^2=1-2\sqrt{2}\frac{\sqrt{6}+\sqrt{2}}{4}+2=2-\sqrt{3}.$
Further, by the Law of Sines in $\Delta DCD',$
$\displaystyle\frac{1}{\sin^{2}\angle CDD'}=\frac{2-\sqrt{3}}{(\sqrt{6}-\sqrt{2})/4}=4,$
implying $\angle CDD'=30^{\circ}.$
Note that $\angle ADD'=30^{\circ}$ also because, by the construction, $\angle DAD'=120^{\circ}$ and $AD=AD'.$ It follows that $\angle ADC=60^{\circ}.$
Solution 2
Thinking of the points as complex numbers, choose $\displaystyle B=-\frac{2}{\sqrt{5}},$ $\displaystyle C=\frac{3}{\sqrt{5}},$ $\displaystyle D=\frac{i}{\sqrt{5}}.$ With this choice, $\displaystyle A=\frac{1}{2\sqrt{5}}+i\frac{\sqrt{5}}{2\sqrt{3}}.$
With $\phi=\angle ADC,$ $\displaystyle\frac{A-D}{C-D}=\frac{AD}{CD}(\cos\phi+i\sin\phi)$ such that $\displaystyle\tan\phi=\frac{Im\left(\frac{A-D}{C-D}\right)}{Re\left(\frac{A-D}{C-D}\right)}.$ Thus, we get
$\displaystyle\frac{A-D}{C-D}=\frac{1}{20\sqrt{3}}[(\sqrt{3}+i(5-2\sqrt{3}))(3+i)]=\frac{\sqrt{3}-1}{4\sqrt{3}}(1+i\sqrt{3}),$
from which $\tan\phi=\sqrt{3},$ i.e., $\phi=60^{\circ}.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579824
