Three Euler Lines That Are Four
Problem
$ABC$ is an equilateral triangle; for a point $P,$ not a vertex of $\Delta ABC,$ consider three triangles. $ABP,$ $BCP,$ $CAP$ and their Euler lines.
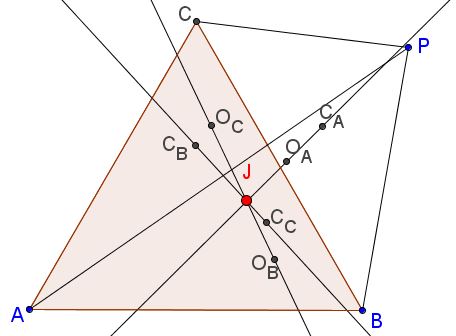
Prove that the three Euler lines concur at a point ($J$ in the diagram.)
In the diagram, $O_A,$ $O_B,$ $O_C$ and $C_A,$ $C_B,$ $C_C$ are the circumcenters and the centroids of triangles $BCP,$ $CAP,$ and $ABP,$ respectively.
Solution
The solution depends very much on a 2001 paper by Antreas P. Hatzipolakis, Floor van Lamoen, Barry Wolk, and Paul Yiu, where they , in particular, proved the Theorem
Let $P$ be a point in the plane of triangle $ABC$ such that the Euler lines of the component triangles $PBC,$ $APC$ and $ABP$ are concurrent. Then the point of concurrency also lies on the Euler line of triangle $ABC.$
In other words, if Euler lines of three of the four triangles $ABC,$ $PBC,$ $APC$ and $ABP$ are concurrent, the all four are. (They also found the locus of point $P$ that satisfies that condition.)
Back to the problem at hand, the Euler lines of, say, triangles $APC$ and $ABP$ meet, even if at a point at infinity. Since $\Delta ABC$ is equilateral, all its centers (circumcenter $O,$ centroid $C,$ orthocenter $H,$ 9-point center $N,$ and others coincide. The Euler line may be said to be undefined, which could be interpreted as nonexistent, or as multiply, not uniquely, defined. Choosing the latter interpretation, any line through the center of an equilateral triangle could be taken as the Euler line. Let's pick the one that passes through the intersection point of $APC$ and $ABP.$ This gives us three concurrent Euler lines. By the theorem mentioned above all four Euler lines are concurrent.
References
- A. P. Hatzipolakis, F. van Lamoen, B. Wolk, P. Yiu, Concurrency of Four Euler Lines, Forum Geometricorum, Volume 1 (2001) 59-68.
Acknowledgment
The problem and the proof have been posted by Antreas Hatzipolakis at the CutTheKnotMath facebook page
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73567291
