 |
Cut The Knot!by Alex Bogomolny |
Freaky LinksWilliam A. McWorter Jr. | |
February 2001
Did you know that recreational mathematics is responsible for crystal clear communications over noisy channels? What would W. Hardy say if he had lived to see his harmless love, number theory, the subject of heated debate over providing modern encryption technology to foreign countries?
It is continuously fascinating how mathematics impinges on itself and the sciences in unexpected and bizarre ways. This page is a small illustration of this phenomenon.
Take a look at the triangular grid T. The plane can be tiled with copies of an equilateral triangle. The vertices of these triangles form the triangular grid. Chinese checkers and a strategy game called Hex are played on these points on boards which are finite portions of the triangular grid.
Fairly familiar stuff. But did you know that the triangular grid is also a quasigroup? That the triangular grid is a block design? And with just a little more effort, that T can produce infinitely many quasigroups and infinitely many block designs?
A quasigroup is a set Q, together with a binary operation *, such that the equations
Examples of quasigroups are, the integers Z with operation + and the nonzero real numbers R with operation · (real multiplication). These two examples have associative operations, and are called groups. A non associative example of a quasigroup is exhibited by the table below, a child of the triangular grid, as we shall see later.
| * | | | a | b | c |
|---|---|---|---|---|
| --- | | | --- | --- | --- |
| a | | | a | c | b |
| b | | | c | b | a |
| c | | | b | a | c |
The table means a * a = a, a * b = c, b * c = a, etc. For this quasigroup
The definition of a quasigroup Q forces its operation table to have the property that every element of Q appears exactly once in every row and column of the operation table. Such a table is known as a latin square.
Latin squares were first investigated by Leonhard Euler as "un nouveau espèce de carré magique", a kind of magic square. Thus latin squares began as a part of recreational mathematics, but now are an integral part of a fundamental branch of mathematics called combinatorics.
Quasigroup, latin square? How can the triangular grid produce such a thing?
A block design is a family of sets, called blocks, satisfying certain conditions. All blocks have the same number of elements, every element occurs in the same number of blocks, and every pair of elements occurs in the same number of blocks. A block design with finitely many elements is called a balanced incomplete block design. It is a set of v elements and a family of b subsets of the v elements, called blocks, such that every block has k elements, every element occurs in r blocks, and every pair of elements occurs in λ blocks. The numbers v, b, r, k, and λ are called the parameters of the design. Here is an example of a balanced incomplete block design with parameters
{1,2,3}, {1,2,4}, {1,3,5}, {1,4,6}, {1,5,6}, {2,3,6}, {2,4,5}, {2,5,6}, {3,4,5}, {3,4,6}.
Balanced incomplete block designs also began as a recreational pursuit when T. P. Kirkman posed his famous Schoolgirl Problem. Now, like latin squares, balanced incomplete block designs are a basic subject of combinatorics (see britannica.com for more on latin squares, block designs, Kirkman's Schoolgirl problem, and combinatorics in general).
A family of sets? In what way can the triangular grid yield a family of sets?
Glad you asked. Consider any two points p and q on the triangular grid T. A clockwise rotation of T through 60° about the point p maps T onto itself. Thus q is mapped onto a point r of T. The triangle pqr is equilateral. Similarly, rotating 60° clockwise about q maps p onto a point s of T so that pqs is an equilateral triangle. Thus any two points p and q of T are vertices of exactly two equilateral triangles whose vertices are points of the triangular grid T. This regularity of pairs of points in T is what enables the interpretation of T as a quasigroup and a block design.
The points of the triangular grid T form an infinite block design whose blocks are all triples of grid points which are vertices of equilateral triangles. Every block has
We can also use the pair regularity of T to turn it into quasigroup. For each pair p and q of points of T, define a binary operation * on T by,
So far T has provided us with one block design and one quasigroup. To squeeze more designs and quasigroups from T, we invoke the notion of factor group from group theory. Let u be the unit vector
Let f be the 60° clockwise rotation about the origin
f(sp) = sf(p), for all integers s and points p of T,
| f(f(xu + yv)) - f(p) + p | = f(xf(u) + yf(v)) - f(p) + p |
| = f(x(u - v) + yu) - f(p) + p | |
| = x(f(u) - f(v)) + yf(u) - f(p) + p | |
| = x(u - v - u) + y(u - v) - f(p) + p | |
| = -xv + yu - yv - f(xu + yv) + xu + yv | |
| = x(u - v) + yu - xf(u) - yf(v) | |
| = x(u - v) + yu - x(u - v) - yu | |
| = (0, 0). |
Let's look at some of the properties of the quasigroup operation *. The rotation f fixes the origin
p * p = p + f(p - p) = p + f(O) = p + O = p.
A quasigroup Q is idempotent if every element x in Q satisfies
Also, for any points p and q in T, the points p, q, and
Remarkably, even though T under * is not associative, left multiplication by an element of T induces an automorphism of T as a quasigroup. A function F on a quasigroup Q is an automorphism if F is a 1-1 map from Q onto Q such that
The triangular grid T under the operation * is also anticommutative; i.e., whenever p≠q, then
Ok. Now let's look at what the triangular grid has to say about finite quasigroups and finite block designs. Our construction is due to our host, Alexander Bogomolny. The author's original construction is a limited special case of Bogomolny's idea. (A note from A.B.: The insight for my contribution has originated with a flash recollection of the plane tessellation induced by Napoleon's theorem.)
Let a and b be integers, not both zero. Select vectors
f(-b, a + b) = -bf(u) + (a + b)f(v) = -b(u - v) + (a + b)u = au + bv = (a, b).
Let H be the subgroup of T generated by these two vectors. The factor group T/H, consisting of the cosets of H, is a finite group of order
The factor group T/H is also a quasigroup under the operation * defined on the cosets of H by
(H + p) * (H + q) = H + p * q.
Before proving that * is well-defined and other needed properties, let's look at some small examples.
Let a = b = 1. Then a2 + ab + b2 = 3 and the cosets of T/H are H,
| * | | | H | H + (1, 1) | H + (2, 2) |
|---|---|---|---|---|
| ---------------- | | | ---------------- | ---------------- | ---------------- |
| | | H | H + (2, 2) | H + (1, 1) | |
| H + (1, 1) | | | H + (2, 2) | H + (1, 1) | H |
| H + (2, 2) | | | H + (1, 1) | H | H + (2, 2) |
We can form this table by using the formal definition of * on T/H, or we can perform the calculation geometrically. Just do * in T and replace the elements obtained by the cosets of H containing them. We do this with our next example, with the help of a handy applet.
Let a = 2 and b = 0. Then the corresponding subgroup H of T has 4 cosets, H, abbreviated 4,
| * | | | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| --- | | | -- | --- | --- | --- |
| 1 | | | 1 | 3 | 4 | 2 |
| 2 | | | 4 | 2 | 1 | 3 |
| 3 | | | 2 | 4 | 3 | 1 |
| 4 | | | 3 | 1 | 2 | 4 |
We can see how this table is obtained by considering the portion of the triangular grid below, with its points labelled by the coset of H that contains the point.
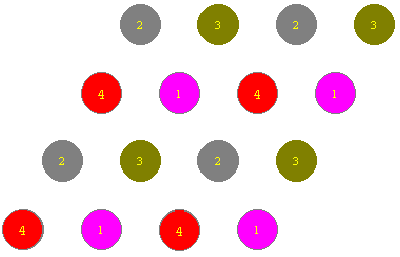
To compute a product, we compute as we would with the points of T, except that we label the result by the coset of H containing the result of the computation. For example, look at the first 4 and 1 in the last row of the display above. By the definition of * on T,
The block design associated with this quasigroup has parameters
{1, 2, 1 * 2) = {1, 2, 3}, {1, 3, 1 * 3} = {1, 3, 4},
This design is not new. In fact, it is trivial. It is all 3-element subsets of a 4-element set. For other choices for a and b we get non-trivial block designs, as long as
Block designs for k = 3 and λ = 2 are known for all feasible parameters v, b, and r. So none of the block designs constructed here settle any unknown cases. Nor do these designs cover all feasible parameters. The example of a design shown first in this article has
Suppose we wish to schedule a round robin chess tournament among 6 players so that every player plays every other player exactly once with the black pieces. That's 30 games altogether. To spread things out somewhat, we'd like there to be three games a day for three players. A partial solution without regard to who plays who with what pieces is provided by the block design given at the beginning of this page. It turns out that this block design permits choosing who plays who each day so that each player plays every other player exactly once with the black pieces. A complete solution is displayed below.
| Blocks | Games | |
|---|---|---|
| {1, 2, 3} | b 1 2 3 w 2 3 1 | |
| {1, 2, 4} | b 2 1 4 w 1 4 2 | |
| {1, 3, 5} | b 1 3 5 w 3 5 1 | |
| {1, 4, 6} | b 4 1 6 w 1 6 4 | |
| {1, 5, 6} | b 1 5 6 w 5 6 1 | |
| {2, 3, 6} | b 3 2 6 w 2 6 3 | |
| {2, 4, 5} | b 2 4 5 w 4 5 2 | |
| {2, 5, 6} | b 2 6 6 w 5 5 2 | |
| {3, 4, 5} | b 3 5 5 w 4 4 3 | |
| {3, 4, 6} | b 4 3 4 w 3 6 6 |
For example, the day players 1, 2, and 3 play, 1 plays 2 with the black pieces, 2 plays 3 with the black pieces, and 3 plays 1 with the black pieces. Each player plays two games that day with one rest break.
Conveniently, all of the designs derived from the triangular grid allow the construction of round robin chess tournament schedules. In fact, all these designs are what are known as Mendelsohn triple systems, block designs with block size 3 and
Let a = 2 and b = 1. Then the corresponding subgroup H has

{1, 2, 7}, {2, 1, 5}, {1, 3, 6}, {3, 1, 7},
The elements of the blocks above are listed in such a way that, if you order the elements of each block cyclically from left to right, you get a schedule for a round robin tournament for 7 players, with each player playing every other player exactly once with the black pieces.
Reference
- Th. Beth, D. Jungnickel and H. Lenz, Design Theory, Cambridge University Press, Cambridge, vols 1 and 2, 1999.
- W. D. Wallis, Combinatorial Designs, Monographs and Textbooks in Pure and Applied Mathematics, 118, (1988)
Freaky Links
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73581511
