A. Bogomolny

Following is the diagram I used in one of the emails to W. McWorter as an argument in support of the claim that there must exist some kind of factorization that leads to a variety of finite quasigroups.

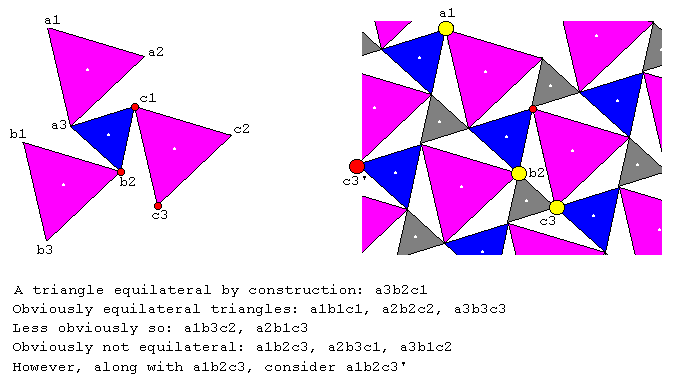
It's not at all obvious (and in fact, at the time, it was not obvious to me) what that diagram had to do with the claim. In hindsight, I can see three elements, say, a1, b1, c1, such that b1 * a1 = c1. Assume each of the three elements changes over a triangular subgrid (signified, for element a1, by the triangle a1a2a3). The subgrids over which elements a1, b1, c1 change do not coincide, but are isomorphic (which may be surmised from the congruence of triangles a1a2a3, b1b2b3, and c1c2c3.) What the verbal part of my message says is that the identity b1 * a1 = c1 holds "subgrid wise".

It's to Professor McWorter's credit that he developed the right idea from a vague representation of an obscure intuition.

Freaky Links

• Fill the Grid
• Napoleon's Plane Tessellation
• T/H is a Quasigroup

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny