What Is the Extremal Principle?

The Extremal Principle is a methodology, a useful problem solving tactics, wherewith one seeks a solution to a problem among possible candidates that satisfy some extreme conditions within the parameters of the problem.

There are $N$ points in the plane such that the area of a triangle formed by any three of the points does not exceed $1.$ Prove that there is a triangle of area not more than $4$ that contains all $N$ points.

Solution

There are ${N \choose 3}$ triangles that could be formed with $N$ points - a finite number in any event. Let $ABC$ be one of the triangles with the maximum area. (Its area is still does not exceed $1.)$ Let $A'B'C'$ be its anticomplementary triangle, i.e., the triangle formed by the parallels to the sides of $\Delta ABC$ and passing through its vertices. (This makes $ABC$ the medial triangle of $\Delta A'B'C'.)$

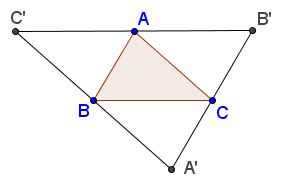
anticomplementary triangle

The area of $\Delta A'B'C'$ is four times that of $\Delta ABC$ and, therefore, does not exceed $4.$ I am going to prove that $A'B'C'$ contains all $N$ given points. Assume to the contrary that there is point $P$ (from the set) that lies outside $\Delta A'B'C'.$ Each of the side lines of the latter divides the plane into two half-planes with the triangle itself in one of the halves. Point $P$ could not be on the same side as the triangle for all three side lines, for then it would lie inside the triangle. Without loss of generality, assume that line $A'B'$ separates $P$ from $\Delta A'B'C':$

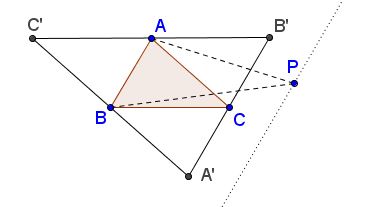
anticomplementary triangle - solution to a problem

But then the area of $\Delta ABP$ is bigger than that of $\Delta ABC$ which contradicts the selection of $\Delta ABC.$ The contradiction proves the statement.

Here's an absolutely classical example:

Natural numbers are written in the cells of a regular (square, triangular, hexagonal) grid such that every number is the average of the numbers in the adjacent cells. Prove that all numbers are equal.

Solution

Any set of natural numbers has a minimal element. Since, according to one of the readings of the Pigeonhole Principle, the least value is at most the average, all the neighbors of our minimal number must be equal to that number. The same in turn holds for their neighbors and for the neighbors of the neighbors and so on. (This of course needs to be verified that in this manner all the cells get accounted for.)

In the context of the Extremal Principle, the term "extreme" has a most broad interpretation; its essence is to look among the least common candidates. Sometimes, especially in the Russian literature, this problem solving tactics is called the Principle of Narrow Places ("tight circumstances or confines" may be a translation closer in the meaning.) A typical example is the question about covering a chess board with domino: is it possible to avoid creating a $2\times 2$ square? The answer comes from studying how the dominoes can be fitted in a chessboard corner, where there is less freedom of placing the pieces than anywhere else.

By association, the literal, physical interpretation of the expression "narrow place" leads to an extension of the method. "Narrow places" - this is where you'd be looking to build a bridge over a ravine or jump over a big puddle. So, sometimes it is useful to consider two opposite extremes and then show that the solution to the problem lies somewhere on a "bridge" between the two.

Is it possible to find $1000$ consecutive numbers among which there are exactly $5$ primes?

Solution

Clearly there is nothing special about $1000$ or $5.$ What can be said in general about the amount of primes among consecutive numbers? One fact comes to mind: there are runs of successive composite numbers of any length. May this be used? Well, yes, through this insight: shifting (up or down) a prime-free run by $1$ may add at most one prime. So it is likely that there are long runs with exactly one prime; and then also two primes - but then it becomes trickier: while shifting the sequence, we can gain a prime at one end and lose one at the other. So caution needs to be exercised. But which direction we should go. Certainly "up" as at the beginning the run contained no primes at all. How far? There are 168 primes among the first 1000 integers. So, moving towards this sequence from a far away run with no primes and adding (or not) a prime at a time, we are bound to reach 168 primes at the end. Since the amount of primes in a run grows by at most $1,$ we shall eventually encounter all numbers from $0$ to $168$ in a nondecreasing sequence with no gaps; sooner or later we'll get a $5.$

Further examples

References

M. Aigner, G. Ziegler, Proofs from THE BOOK, Springer, 2000
C. Alsina, R. B. Nelsen, Charming Proofs, MAA, 2010
H. S. M.Coxeter, Introduction to Geometry, John Wiley & Sons, 1961
M.Gardner, Time Travel and Other Mathematical Bewilderments, W.H.Freeman & Co., 1988.

71544907