Number of Regions N Lines Divide Plane
Below I give two solutions to a well-known problem. One standard, the other - in my view - beautiful.
What is the maximum number $L_n$ of regions defined by $n$ lines in the plane?
Solution 1
We find and then solve a recursive formula for $L_n,$ see [Concrete Mathematics, 4-8].
Obviously $L_0=1$ and $L_1=2.$ Short experimentation will convince you that $L_2=4.$ However, the next number that intuition often suggests, i.e., $L_3=8$ does not hold. Instead, $L_3=7.$ Why so? This is because, if we want to obtain the maximum possible number of regions, we shall not let the new line pass through the intersection of the first two, for then we would get six regions and can do better. Leaving that point on one side of the third line means that the line won't be able to cross all four already existent regions, but at most only three - one more than there are lines. This gives a clue to a general case.
When adding a line, the latter may cross the existent ones in so many distinct points and thus cross (and divide) so many existent regions. On reflection, $L_{n+1}=L_{n}+(n+1). Further,
$\begin{align}\displaystyle L_{n+1}&=L_{n}+(n+1)\\ &=L_{n-1}+[n+(n+1)]\\ &=L_{n-2}+[(n-1)+n+(n+1)]\\ &\space\cdots\\ &=L_{2}+[3+\ldots +(n-1)+n+(n+1)]\\ &=L_{1}+[2+3+\ldots +(n-1)+n+(n+1)]\\ &=L_{0}+[1+2+3+\ldots +(n-1)+n+(n+1)]\\ &=1+[1+2+3+\ldots +(n-1)+n+(n+1)]=1+\frac{(n+1)(n+2)}{2}. \end{align}$
In other words, $\displaystyle L_{n}=\frac{n(n+1)}{2}+1=\frac{n^{2}+n+2}{2}.$
Solution 2
This solution [Engel, p. 40] starts with an observation that the regions into which the plane is divided by $n$ lines, are defined by their vertices which are the points of intersection of the given lines. We may assume that none of the lines is horizontal; otherwise, rotate the plane by a small angle. This ensures that the regions are of two sorts: some regions (finite or not) have the lowest vertex, others do not.
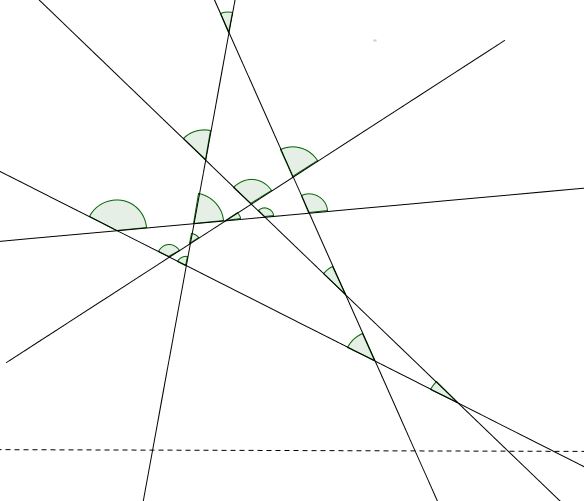
Every point of intersection serves as the lowest vertex of exactly one region. Therefore, for $n$ lines, there are $\displaystyle\frac{n(n-1)}{2}$ regions of the first sort. There are $n+1$ regions of the second sort, which becomes apparent when a horizontal line is drawn that crosses all $n$ lines below all of their "legitimate" intersection points. Therefore, $\displaystyle L_{n}=\frac{n(n-1)}{2}+n+1={n\choose 2}+{n\choose 1}+{n\choose 0}.$
The latter expression can be easily generalized to a $3D$ problem wherein the question is about the number of regions into which $n$ planes divide the space. The answer is $\displaystyle {n\choose 3}+{n\choose 2}+{n\choose 1}+{n\choose 0}.$
As we've seen, the solution employs the 1-1 correspondence between the regions that have the lowest vertex and the set of all points of intersection of the given lines by assigning to each such region its lowest (extreme) vertex. For this reason, A. Engel treats the solution as an application of the Extremal Principle in problem solving. Which just shows the breadth of the contexts in which the principle proves to be a useful tool.
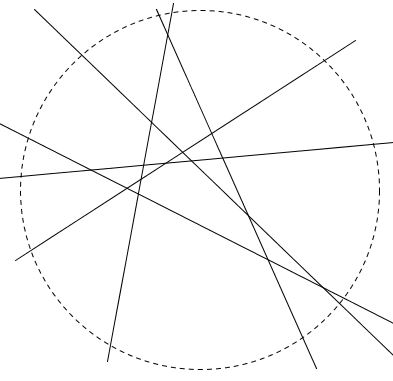
Note also that the same formula gives the maximum number of regions into which $n$ lines divide a circle. This is because the number of intersections of the lines is finite and can be included into a circle dividing it into as many regions as their were in the division of the plane.
References
- A. Engel, Problem-Solving Strategies, Springer Verlag, 1998
- R. Graham, D. Knuth, O. Patashnik, Concrete Mathematics, 2nd edition, Addison-Wesley, 1994
|Contact| |Front page| |Contents| |Algebra| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73609371
