What Is Analytic Geometry?

Analytic Geometry is a branch of algebra that is used to model geometric objects - points, (straight) lines, and circles being the most basic of these. Analytic geometry is a great invention of Descartes and Fermat.

In plane analytic geometry, points are defined as ordered pairs of numbers, say, (x, y), while the straight lines are in turn defined as the sets of points that satisfy linear equations, see the excellent expositions by D. Pedoe or D. Brannan et al. From the view of analytic geometry, geometric axioms are derivable theorems. For example, for any two distinct points (x₁, y₁) and (x₂, y₂), there is a single line ax + by + c = 0 that passes through these points. Its coefficients a, b, c can be found (up to a constant factor) from the linear system of two equations

ax₁ + by₁ + c = 0
ax₂ + by₂ + c = 0,

or directly from the determinant equation

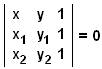However, no axiomatic theory may escape using undefined elements. In Set Theory that underlies much of mathematics and, in particular, analytic geometry, the most fundamental notion of set remains undefined.

Geometry of the three-dimensional space is modeled with triples of numbers (x, y, z) and a 3D linear equation ax + by + cz + d = 0 defines a plane. In general, analytic geometry provides a convenient tool for working in higher dimensions.

Within the framework of analytic geometry one may (and does) model non-Euclidean geometries as well. For example, in plane projective geometry a point is a triple of homogenous coordinates (x, y, z), not all 0, such that

(tx, ty, tz) = (x, y, z),

for all t ≠ 0, while a line is described by a homogeneous equation

ax + bx + cz = 0.

In analytic geometry, conic sections are defined by second degree equations:

ax² + bxy + cy² + dx + ey + f = 0.

That part of analytic geometry that deals mostly with linear equations is called Linear Algebra.

Cartesian analytic geometry is geometry in which the axes x = 0 and y = 0 are perpendicular.

The components of n-tuple x = (x₁, ..., x_n) are known as its coordinates. When n = 2 or n = 3, the first coordinates is called abscissa and the second ordinate.

References

D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988

72103951