An Inequality between AM, QM and GM
Problem
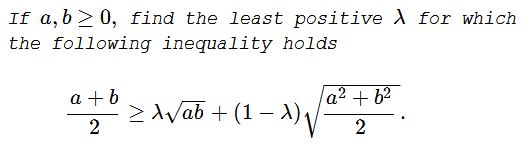
Solution
Without loss we can assume $ab=1$, otherwise multiply numerator and denominator by $\displaystyle \frac{1}{\sqrt{ab}}$, which amounts to replacing $a,b$ by $\frac{a}{\sqrt{ab}}, \frac{b}{\sqrt{ab}}$.
$\displaystyle \begin{align} 1-\lambda &= \frac{\frac{a+a^{-1}}{2} - 1}{\sqrt{\frac{a^2+a^{-2}}{2}}-1} \\&= \frac{\cosh(t) - 1}{\sqrt{\cosh(2t)}-1} \qquad (e^t = a) \\&= \frac{\cosh(t) - 1}{\sqrt{2\cosh^2(t)-1}-1} \\&= \frac{s - 1}{\sqrt{2s^2-1}-1} \qquad (s = \cosh(t) \geq 1) \\&= \frac{1 - s^{-1}}{\sqrt{2-s^{-2}}-s^{-1}} \end{align}$
The last term reaches its maximum at $\displaystyle\lim_{s\to\infty} \frac{1 - s^{-1}}{\sqrt{2-s^{-2}}-s^{-1}} = \frac{1}{\sqrt{2}}$, hence
$\lambda \geq 1 - \frac{1}{\sqrt{2}}.$
Acknowledgment
Leo Giugiuc has kindly communicated to me the above problem, along with a solution of his. According to Kadir Altintas, the problem was offerred at the 2017 Hong Kong math olympiad. The above solution is by Long Huynh Huu. This solution has a subtle error which is explained by Long Huynh Huu on a separate page. There are two correct solutons: Leo's and Long's.
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73584419
