Two Circumcircles And Two Pairs of Parallels
What is this about?
A Mathematical Droodle

The applet may suggest the following statement:

Let point P lie on a side AB of ΔABC. Circle C(A) is the circumcircle of ΔAPC. Circle C(B) is the circumcircle of ΔBPC. Q is an arbitrary point on the segment AB. Points A' on C(B) and B' on C(A) lie on the same side of AB as C such that QA'||AC and QB'||BC.

Two circles and two parallels, problem

Show that

Quadrilateral PQA'B' is cyclic and
Points A', C, B' are collinear.

(This is problem #3 from the 34^th USA Mathematical Olympiad, 2005. One solution has been published in Math Magazine, v 79, n 2, April, 2006, p. 160. The whole collection of problems from the 2005 USAMO, Team Selection Test, and IMO have been also published by MAA.)

Proof

Assume points A, P, Q, B follow in this order. Other configurations can be treated similarly. Denote the angles of ΔABC at A α and and B β. Assume that A' has been constructed as above and let B'' be the intersection of CA' with C(A) other than C.

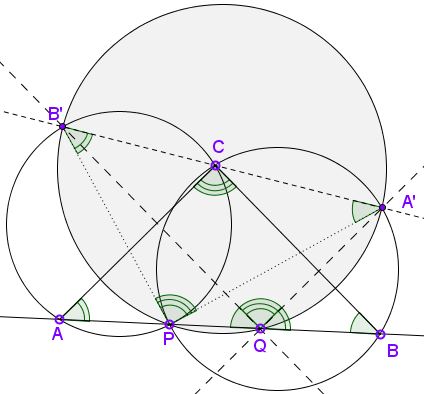
Two circles and two parallels, solution

Angles CAP and CB''P are equal as being inscribed in the same circle and subtended by the same chord. Angles CAP and A'QB are equal because QA'||AC:

∠CB''P = α = ∠A'QB.

It follows that the sum of angles A'QP and A'B''P is 180° so that quadrilateral PQA'B'' is cyclic. Therefore,

(1)

∠PQB'' = ∠PA'B''.

Further, since CPBA' is cyclic,

(2)

∠PA'B'' = ∠PA'C = ∠PBC = β.

From (1) and (2) we obtain BC||QB'' and that in fact B'' = B'.

References

Z. Feng et al (ed.), USA and IMO Olympiads 2005, MAA, 2006

71536744

Two Circumcircles And Two Pairs of ParallelsWhat is this about? A Mathematical Droodle

Proof

References

Two Circumcircles And Two Pairs of Parallels
What is this about?
A Mathematical Droodle