Equidecomposition of a Rectangle and a Square:
What is this about?
A Mathematical Droodle
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyThe applet purports to illustrate a simple fact:
A rectangle can be cut into several pieces which, after translation and rotation, combine into a square of equal area.
The applet only demonstrates this fact for sufficiently elongated rectangle. Rectangles that are nearer a square to start with can be cut into strips that combine into rectangles of the sort the applet handles well, i.e., in which the length is at least twice its width.
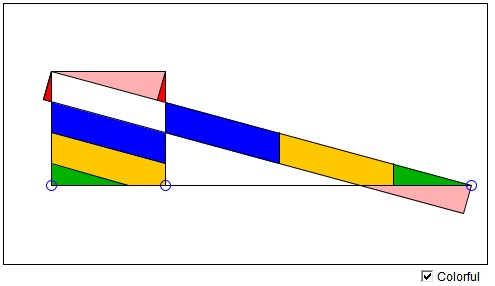
Since every triangle is equidecomposable with a rectangle, we can also claim that every triangle is equidecomposable with a square! An even more obvious conclusion is that two rectangles of equal area are equidecomposable. This fact can be established directly and likely in a more economical manner.
(The problem of constructing a square equal in area to a given rectangle has been solved by Euclid's Elements II.14.)
References
- G. Frederickson, Dissections: Plane & Fancy, Cambridge University Press, 1997, p. 222
Equidecomposition by Dissiection
- Carpet With a Hole
- Equidecomposition of a Rectangle and a Square
- Equidecomposition of Two Parallelograms
- Equidecomposition of Two Rectangles
- Equidecomposition of a Triangle and a Rectangle
- Equidecomposition of a Triangle and a Rectangle II
- Two Symmetric Triangles Are Directly Equidecomposable
- Wallace-Bolyai-Gerwien Theorem
- Perigal's Proof of the Pythagorean Theorem
- A Proof Perigal and All Others After Him Missed
- Dissection of a Vase
- Curvy Dissection
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73585394
