Dissection of a Vase
What is this about?
A Mathematical Droodle

Discussion

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet is intended to help raise and answer a question about a shape (that might remind one of a vase) whose border consists of six quarter circles drawn with the same radius:

Given the radius, say R, of the arcs, what is the area of the vase?

The top of the vase if complemented by four circular sectors with central angle of 90°

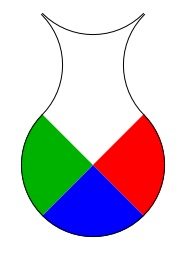
becomes a square of the side equal to the diameter of the arcs and circles, i.e., 2R.

One of the sectors (the lowest) is already inside the intended square; the other three find there locations by dragging the scroll bar and come from the remaining three quarters of a circular part of the vase. It follows that - by dissection - the area of the vase equals that of the square.

References

1. I. Moskovich, Leonardo's Mirror and Other Puzzles, Dover, 2011

Equidecomposition by Dissiection

• Carpet With a Hole
• Equidecomposition of a Rectangle and a Square
• Equidecomposition of Two Parallelograms
• Equidecomposition of Two Rectangles
• Equidecomposition of a Triangle and a Rectangle
• Equidecomposition of a Triangle and a Rectangle II
• Two Symmetric Triangles Are Directly Equidecomposable
  • Two Symmetric Triangles Are Directly Equidecomposable II
  • Two Symmetric Triangles Are Directly Equidecomposable III
  • Two Symmetric Triangles Are Directly Equidecomposable IV
• Wallace-Bolyai-Gerwien Theorem
• Perigal's Proof of the Pythagorean Theorem
• A Proof Perigal and All Others After Him Missed
• Dissection of a Vase
• Curvy Dissection

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny