This proof is based on the tessellation that was known to Dudeney, Perigal, and even earlier to Annairizi of Arabia (ca. 900 A.D.) Miquel Plens - a high school student from Catalonia - placed himself in line of the great predecessors by giving the proof a novel twist.
Pythagorean Theorem by Tessellation
Miquel Plens, Catalonia
10 Oct, 2012
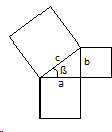
We've got a right triangle with a square in each side. With the squares in the legs, we make a mosaic, combining the same number of squares from each leg. I did it with eight squares, because it was the closest to a square, and it was easier.

Then, we make the same with eight hypotenuse squares:

Then, we put together both mosaics, and their sides form the same angle as in the original right triangle:
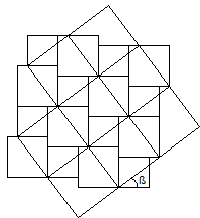
We can see that both mosaics have some pieces that don't match, so we separate them:
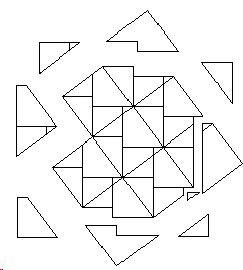
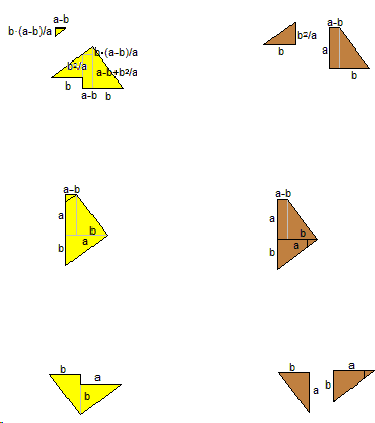
The yellow pieces are the pieces from the hypotenuse which don't match, and the Brown ones are the legs' pieces which don't match. So, we can conclude that eight hypotenuse's squares are equal to eight short leg's squares plus eight long leg's squares, which divided by eight makes the Pythagorean theorem.
![]()
|Contact| |Front page| |Contents| |Geometry| |Pythagorean Theorem|
Copyright © 1996-2018 Alexander Bogomolny73589507
