Two Simsons in a Triangle
What Is This About?
A Mathematical Droodle
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
The applet attempts to illustrate a generalization of a property of the simsons corresponding to two diametrically opposite points on a circumcircle of a triangle:
For two diametrically opposite points on a circumcircle of a triangle the two simsons are perpendicular. The simsons of any two points P and Q on a circumcircle of ΔABC meet at an angle equal to one of the angles formed by P and Q and one of the vertices of the triangle. The proof below is by Hubert Shutrick.
| What if applet does not run? |
More accurately, let sP and sQ be the simson lines of points P and Q and M the intersections of the two. P lies on an arc of the circumcircle opposite one of the vertices A, B, or C which we'll denote vP and similarly introduce vQ. If
Define also, S to be the intersection of sP and vQ and T the intersection of sQ and vP. What Professor Shutrick has found is that the quadrilateral MSVT is cyclic. The proof depends on a particular configuration of the five points A, B, C, P, Q. Below we shall consider just one case:
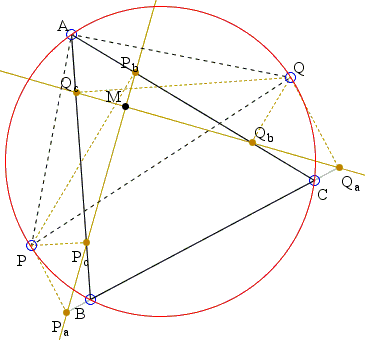
In this case, V = A, S is the intersection of sP and AQ and T is the intersection of sQ and AP. Other notations have been borrowed from the case of diamterically opposite P and Q.
Since quadrilaterals APbPcP and AQcQbQ are cyclic,
∠PAPc = ∠PPbPc and
∠QAQb = ∠QQcQb.
By the construction, ∠APbP = ∠AQcQ = 90° implying that in quadrilateral APbMQc,
| ∠QcMPb | = 360° - ∠BAC - ∠APbM - ∠AQc | |
| = 360° - ∠BAC - (90° + ∠PPbPc) - (90° + ∠QQcQb) | ||
| = 180° - ∠BAC - ∠PAPc - ∠QAQb) | ||
| = 180° - ∠PAQ. |
From here, ∠SAT + ∠SMT = 180° and the quadrilateral ASMT is indeed cyclic.
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73580207
