Problem 2 from the IMO 2007, Second solution

Here is Problem 2 from the IMO 2007:

Consider five points A, B, C, D and E such that ABCD is a parallelogram and BCED is a cyclic quadrilateral. Let i be a line passing through A. Suppose that l intersects the interior of the segment DC at F and intersects line BC at G. Suppose also that EF = EG = EC. Prove that l is the bisector of angle DAB.

The solution below is by Vo Duc Dien and is a significant simplification of the solution by Anton Batominovski.

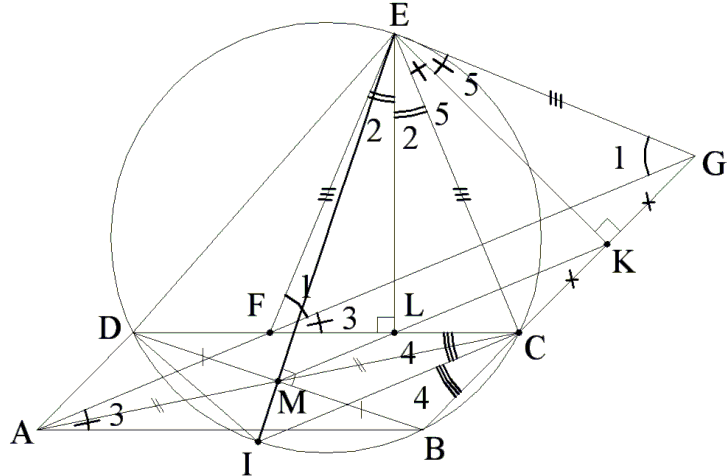
Based on Simson-Wallace's theorem the feet of projections of E down to the three sides of triangle BCD (denoted M, L and K) are colinear as seen on the diagram.

Since L and K are the midpoints of FC and CG, respectively, LK||FG, and in triangle ACG, LK intersects AC at its midpoint M. Since ABCD is a parallelogram, M is also the midpoint of DB.

Therefore, there is only one unique point M to satisfy conditions that M is on DB and also collinear with K and L, and M is also the foot of E to DB.

Extend EM to cut the circle at I. Since EI is perpendicular to DB and DM = BM, it is understood that I is midpoint of arc DB. Therefore ∠DCI = ∠BCI = ∠4, as denoted on the graph. EI is also the diameter of the circle.

It follows that ∠ECI = 90°. Further, ∠ICB = ∠CEK (they both have sides perpendicular to one another), or

From (*), ∠3 = ∠4. In other words, ∠3 = ½∠DCB = ½∠DAB, meaning that AG is the bisector of ∠DAB which is the answer.

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|