Pivot Theorem
The applet below presents a problem. Play with it (there are 6 draggable points) and see if you can come up with a statement the applet purports to illustrate. Whatever theorem you come up with, try proving it before looking into my formulation and its solution. If you come up with anything different from mine, I would like to hear from you.
1 October 2015, Created with GeoGebra
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
My intention was to the following statement:
Let a point be selected on every side of a given a triangle. For every vertex, consider two of the selected points that lie on the sides of triangle that form that vertex. There is a single circle through these three points. In all there are three circles. The theorem states that these three circle meet at a single point.
This theorem is the converse of another one whose solution employed the basic properties of inscribed angles. Roughly speaking that problem reads
Statement A
Given three circles that pass through a single point. Then such-and-such lines form a triangle with vertices on the given circles.
The current problem reverses the premise (three circles pass through a single point) and the conclusion (lines form a triangle) of the theorem:
Statement B
Given a triangle. Then such-and-such circles pass through a single point.
Two statements in which the premise of one appears as the conclusion of the other and vice versa, are known as the converse of each other. In our case, the first statement happens to be a theorem (i.e., a proven statement). This does not automatically imply that the second statement is also provable. In general, it may or may not be a theorem. In this particular situation, the second statement is indeed correct and can be proved. Furthermore, the proof I am aware of is based on the validity of the converse theorem.
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
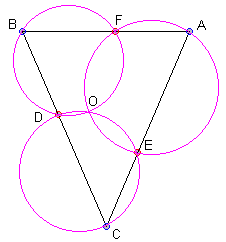
Forget for a moment about one of the given circles. For example, drop the one associated with the vertex B. This leaves us with two circles and a triangle. The two remaining circles share two points: E and O. Through the points O, D and F draw a circle. Now, we are in the position described in Statement A. If we start with the point C, then extend CE till A, from which we draw AF. Likewise, in the other direction, we construct CD. By Statement A, AF and CD meet at a point on the just constructed circle. However, it is a condition of the statement we are proving that AF and CD meet at the vertex B of the given triangle. Therefore, B lies on the circle that passes through three points O, D, and F. But the circle through B, D, and F is the one we erased (apparently only temporarily) at the beginning of the proof. Put another way, the point O (the second intersection of the two circles associated with vertices A and C) belongs two the circle that passes through B, D, and F. This proves Statement B.
For the reference sake, the latter statement is known as the Pivot theorem.
References
- D.Wells, You are a Mathematician, John Wiley & Sons, 1995
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73568204
