A Compass Only Construction:
A Chord Tangent to an Inner circle
I came across the following problem while reading P. Nahin's The Logician and the Engineer.
In two concentric circles, locate parallel chords in the outer circle which are tangent to the inner circle, by the use of compasses only, finding the ends of the chords and their points of tangency.
The engineer in the title is Claude Shannon whose solution to the problem has been published in the American Mathematical Monthly (Vol. 42, No. 1 (Jan., 1935), p. 45).
The applet below illustrates the problem and Shannon's solution. Points \(A\), \(B\), \(C\) are draggable. \(C\) is the common center of two circles \(C(C,A)\) and \(C(C,B)\) - the bigger one passing through \(A\) and the smaller one through \(B\).
|Activities| |Contact| |Front page| |Contents| |Up| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyIt is assumed that the common center of the two circles is given. If it is not given, it may be located by the methods of Mascheroni. The point diametrically opposite a known point on a circle of known radius may be located by "stepping off" the radius three times as a chord from the known point around the circle.
Construction
Select a point \(P\) on the inner circle for one point of tangency, and locate its diametrically opposite point as the other point of tangency. With \(P\) as center, draw a circle through \(C\), the center of the given circles, and locate \(Q\) diametrically opposite \(C\) on this new circle. With \(Q\) as center and the radius of the larger given circle as radius, draw a circle cutting the larger given circle at \(S\) and \(T\). \(ST\) is tangent to the smaller given circle at \(P\). With radius \(CQ\) and centers \(S\) and \(T\) draw arcs cutting the larger arc of the larger given circle at \(S'\) and \(T'\), which will be the ends of the second chord which is tangent to the smaller given circle.
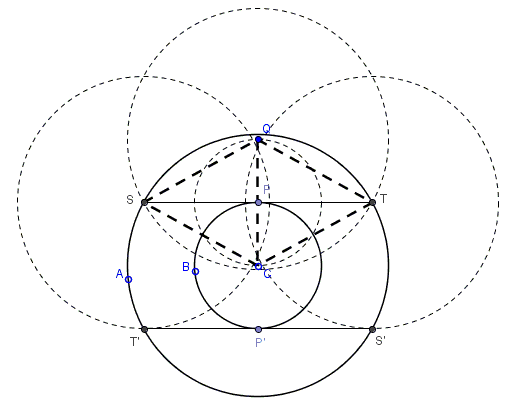
Proof
By construction, \(CQS\) and \(CQT\) are congruent isosceles triangles, so that \(ST\) is the perpendicular bisector of \(CQ\), and hence tangent to the smaller given circle at \(P\). Furthermore, if the circle centered at \(Q\) be "translated" to center at \(C\), it will coincide with the larger given circle, with \(S\) and \(T\) each traveling a distance equal to \(CQ\), and hence falling at \(T'\) and \(S'\) respectively. Consequently, \(STS'T'\) is a rectangle of width \(CQ\), and \(S'T'\) is tangent to the smaller given circle.
Problems (Use a compass only)
- Multiply a Line Segment by a Whole Number
- Reflect a Point in a Line Sgement
- Cross a Circle by a Line Segment
- Drop a Perpendicular to a Line from a Point
- Detect Collinearity
- Complete a Parallelogram
- Bisect an Arc
- Find the Points of Intersection of a Circle with a Line Segment
- Build a Square on a Given Side
- Find the Fourth Proportional of Three Lengths
- Find the Intersection of Two Straight Lines
- Divide a Line Segment into a Whole Number of Parts
- Find the Center of a Given Circle
- Bisect a given line
- Mascheroni Construction of a Regular Pentagon
- A Compass Only Construction - A Chord Tangent to an Inner circle
|Activities| |Contact| |Front page| |Contents| |Up| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73581810
