Constructible Numbers
Examples
René Descartes (1596-1650), considered today as the father of Analytic Geometry, opens his Geometry (La Géométrie, 1637) with the following words:
Any problem in geometry can easily be reduced to such terms that a knowledge of the lengths of certain straight lines is sufficient for its construction. Just as arithmetic consists of only four or five operations, namely, addition, subtraction, multiplication, division and the extraction of roots, which may be considered a kind of division, ... And I shall not hesitate to introduce these arithmetical terms into geometry, for the sake of greater clearness.
Geomtery was the first great step towards algebraization of geometry. The three famous (geometric) problems of antiquity were eventually resolved by algebraic methods. However, the idea did not take off until more than a century and a half later. For example, the last chapter of Disquisitiones Arithmeticae (1801), the premier Gauss' work on the Number Theory, is devoted to the question of constructibility of the heptadecagon (a 17-sided polygon) and other regular polygons with a ruler and a compass. At the time, Gauss felt obliged to explain
The reader may be surprised at encountering such an investigation which at first view appears wholly dissimilar to it; but the exposition will show very clearly the actual relation between this topic and the transcendental arithmetic.
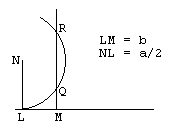
In the Geometry, after pioneering an algebraic notation for an unknown quantity, Descartes gave a geometric solution to the quadratic equation z2 = az - b2. He constructed two perpendicular lines intersecting at point L, and measured NL = a/2 on the vertical line and LM = b on the other. He then drew a circle with the center at N and radius a/2 and a vertical line at M. When the two lines intersect, as on the diagram, he obtained two solutions to the equation:
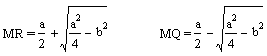
(There is a rather modern incarnation of practically the same approach.)
Probably sensing what may be called the general theory of constructible numbers, he further wrote
And if it can be solved by ordinary geometry, that is, by the use of straight lines and circles on a plane surface, when the last equation shall have been entirely solved there will remain at most only the square of an unknown quantity, equal to the product of its root by some known quantity, increased or diminished by some other quantity also known. Then this root or unknown line can easily be found.
![]()

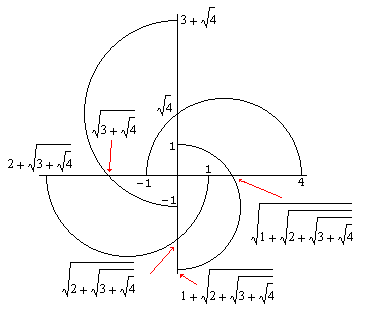

The first diagram depicts the construction for n = 4. I hope that showing the numbers obtained on consecutive steps makes the diagram clear. First draw a semicircle on the segment of
the x-axes between points (-1,0) and (4,0). Its intersection with the yaks occurs at point (0,![]() 4). Extend the second coordinate by 3 and use the new point as the other end of the diameter of the second semicircle. (The first being (0,-1).) Etc.
4). Extend the second coordinate by 3 and use the new point as the other end of the diameter of the second semicircle. (The first being (0,-1).) Etc.
The second diagram shows the construction for n = 124. Unfortunately, there is no room to show all the quantities obtained on every step.
Following is the applet I used to draw the diagrams. The numbers

may have other interesting properties, but there is one you may verify toying with the applet. For any n, the numbers above are less than 2.
| What if applet does not run? |
References
- R. Courant and H. Robbins, What is Mathematics?, Oxford University Press, 1996
- R. Descartes, The Geometry, Great Books of the Western World, Encyclopædia Britannica, 1952
- Oystein Ore, Number Theory and Its History, Dover Publications, 1976
Constructible Numbers, Geometric Construction, Gauss' and Galois' Theories
- Integral Domains: Strange Integers
- Reduction: Constructible Numbers
- Constructible Numbers: Examples
- Four Problems of Antiquity
- A Property of Cubic Equations: Three Problems Of Antiquity
- Angle Trisection
- Squaring the Circle
- Duplication of the Cube
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73581736
