Stern-Brocot Tree

0/1 is a fraction while 1/0 is not. However, using it as such helps describe a way to get all possible positive fractions arranged in a very nice manner. So disguising 1/0 as a fraction has a very good excuse.

We already know how to obtain the mediant of two given fractions. The mediant of two fractions m₁/n₁ and m₂/n₂ is, by definition, the fraction (m₁ + m₂)/(n₁ + n₂). So, for example, from 0/1 and 1/0 we get 1/1. The mediant of 0/1 and 1/1 is 1/2 while the mediant of 1/1 and 1/0 is 2/1. On the next stage of the construction, we form four new fractions: 1/3 from 0/1 and 1/2, 2/3 from 1/2 and 1/1, 3/2 from 1/1 and 2/1, and, finally, the mediant of 2/1 and 1/0 which is 3/1. Continuing this way we get an infinite tree known as the Stern-Brocot tree because it was discovered independently by the German mathematician Moriz Stern (1858) and by the French clock maker Achille Brocot (1860).

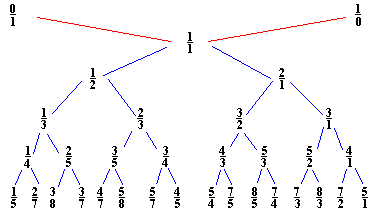
A remarkable thing about Stern-Brocot tree is that it contains all possible non-negative fractions expressed in lowest terms and each exactly once. Just to remind, a fraction m/n is in lowest terms iff m and n are coprime, i.e, iff gcd(n,m)  = 1. To prove this we'll need a series of facts of which the following is the most fundamental: if m₁/n₁ and m₂/n₂ are two consecutive (consecutive in the sense that one of them is a direct descendant of the other) fractions at any stage of the construction then

(1)	m2n1 - m1n2 = 1

This relation is true for the initial fractions: 1·1 - 0·0 = 1. Also, assuming (1) holds for two fractions m₁/n₁ and m₂/n₂, their mediant should satisfy the following two:

n1(m1 + m2) - (n1 + n2)m1 = 1, and m2(n1 + n2) - (m1 + m2)n2 = 1

both of which are equivalent to (1).

Also, if m₁/n₁ < m₂/n₂ then

m1/n1 < (m1 + m2)/(n1 + n2) < m2/n2 ,

from which it follows that the construction of the tree preserves the natural order between the rationals. Therefore, it's impossible to obtain the same fraction twice.

And there is the last point: let a/b be a fraction in lowest terms with a and b positive. I wish to show that this fraction will appear somewhere on the tree. So long as it did not, we shall have

m1/n1 < a/b < m2/n2

for a couple of fractions m₁/n₁ and m₂/n₂ satisfying (1). These are rewritten as

n1a - m1b > 0 and m2b - n2a > 0,

which imply

n1a - m1b 1 and m2b - n2a 1.

from where

(m2 + n2)(n1a - m1b) + (m1 + n1)(m2b - n2a) m1 + n1 + m2 + n2.

An application of (1) yields

a + b m1 + n1 + m2 + n2.

with inevitable conclusion that after at most a+b steps of computing mediants one of them will be equal to a/b.

P.S.

Prof. W.McWorter has offered the following clarification to the proof:

At the root of the tree the minimum numerator-denominator sum (nd sum) is 2. At the first level of the tree the minimum nd sum is 3, and at the n-th level of the tree the minimum nd sum is n+2. To see this, every fraction at the n-th level is the mediant of a fraction at the (n-1)-st level and one at a higher level. The nd sum of a fraction at the (n-1)-st level is at least n+1 and the nd sum of a fraction at a higher level is at least 1. Hence the nd sum of their mediant is at least n+2.

Thus, if a/b is a fraction in lowest terms not equal to any fraction in the tree, then it lies strictly between two consecutive fractions, one of which is at level a+b-1 of the tree (consecutive here is restricted to all fractions constructed up to and including level a+b-1; none constructed beyond this level are considered). Hence by the same calculations a+ba+b+1, a contradiction.

Pierre Lamothe from Canada informed me recently of a property of the Stern-Brocot tree I was unaware of. Pierre discovered that property in his research on music and harmony.

Let's associate with any irreducible fraction p/q the number w(p/q) = 1/pq - its simplicity. The property discovered by Pierre states that the sum of simplicities of all fractions in any row of the Stern-Brocot tree equals 1! We can easily see that this is true for a few first rows:

The inductive proof is based on a fact (proven on later pages) that, for any fraction p/q, two fractions p/(p + q) and (p + q)/q are located just one row below that of p/q. We have an obvious identity:

from which it follows that if the assertion holds for one row, it holds for the next one as well.

Pierre also introduced another function W defined for the members of the tree. For an irreducible fraction p/q, Let N(p/q) denote the row of the tree that contains p/q. We start with N(1/1) = 0, N(1/2) = 1, N(2/1) = 1, N(1/3) = 2, and so on. Then the weighted simplicity W(p/q) is defined as

From the previous statement it then follows that the sum of all weighted simplicities of the fractions on the tree is equal to 1!

References

1. R.Graham, D.Knuth, O.Patashnik, Concrete Mathematics, 2nd edition, Addison-Wesley, 1994.
2. Brian Hayes, Computing Science On the Teeth of Wheels, American Scientist, July-August, Volume 88, No. 4,

• Modular Arithmetic
  • Differences and Similarities
  • Solutions to some problems
• Chinese Remainder Theorem
• Euclid's Algorithm
  • Euclid's Game
  • Binary Euclid's Algorithm
  • gcd and the Fundamental Theorem of Arithmetic
  • Extension of Euclid's Algorithm
  • Stern-Brocot Tree
    • Fine features
    • Binary Encoding
    • Binary Encoding, a Second Interpretation
    • Continued Fractions on the Stern-Brocot Tree
    • Fractions on a Binary Tree
    • Fractions on a Binary Tree II
  • Farey series
    • Farey series, a story
• Pick's Theorem
  • Pick's Theorem, A Proof
  • Farey Series
  • Pick's Theorem Applies to the Farey Series
  • Stern-Brocot Tree
• Fermat's Little Theorem
• Wilson's Theorem
• Euler's Function
• Divisibility Criteria
  • Further examples of divisibility criteria
• Examples
• Equivalence relations
• A real life story

|Contact| |Front page| |Contents| |Algebra| |Store|

Copyright © 1996-2010 Alexander Bogomolny