What Is Determinant?
Given a system of equations
\begin{align} ax + by & = e \\ cx + dy & = f \end{align}
its solution - if exists - is given by the following expressions
\[ x = \frac{de - bf}{ad - bc}, y = \frac{ab - ce}{ad - bc}. \]
(To obtain \(x\), multiply the first equation by \(d\), the second by \(b\) and take the difference. For \(y\), multiply the first equation by \(c\), the second by \(a\) and take the difference.)
The common denominator \(ad - bc\) of the two fractions is known as the determinant of the system of equations, or, more accurately, as the determinant of the matrix \(M = \left (\begin{array}{cc} a & b \\ c & d \end{array}\right )\).
The equation has a unique solution only if its determinant is not \(0\). The determinant of matrix \(M = \left (\begin{array}{cc} a & b \\ c & d \end{array}\right )\) is denoted \(|M|\) or, more explicitly, \(|M| = \left |\begin{array}{cc} a & b \\ c & d \end{array}\right |\).
With a view to a generalization, observe that in the expression \(ad-bc\) there are two products - one with sign plus, the other with sign minus - each of which contains exactly one term from each row and one term from each column! For example, in the term \(bc\), \(b\) comes from the first row, while \(c\) from the second. On the other hand, \(c\) comes from the first column and \(b\) from the second.
For a \(3\times 3\) matrix \( M= \left ( \begin{array}{cc} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{array} \right ) \), the determinant \(|M| = \left | \begin{array}{cc} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{array} \right |\) is defined as
\[ (a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{21}a_{32}a_{13}) - (a_{13}a_{22}a_{31}+a_{12}a_{21}a_{33}+a_{23}a_{32}a_{11}). \]
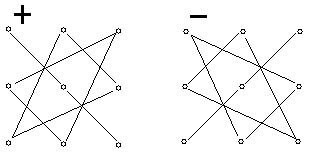
Again, as was the case with a \(2\times 2\) matrix, there are equal amounts of products with sign plus and products with the sign minus, each of which contains exactly one number from every row and one number from every column. The diagrams below may help remember which products come with "+" and which with "-":
A \(2\times 2\) determinant has a very simple geometric meaning. Indeed, \(ad - bc\) is the (signed) area of a parallelogram with vertices at \((0, 0)\), \((a, b)\), \((a+c, b+d)\), \((c, d)\).

The area of the enclosing rectangle is \((a+c)\cdot (b+d)\). To obtain the area of the parallelogram, we need to subtract the area of four triangles and two rectangles. After subtraction, we get exactly \(ad - bc\). The determinant \(\left |\begin{array}{cc} a & b \\ c & d \end{array}\right |\) changes sign when the rows are swapped. This is why the area was designated "signed". It change signs when the vertices are listed in a different order. (There are other pww of this result: one by dissection and one based on the shearing transform.)
The \(3\times 3\) determinant has the meaning of the volume of a parallelopiped defined by three vectors (the rows of the determinant.)
From the definition we may deduce several properties of the determinants:
- If two rows or two columns are equal, the determinant vanishes:
- Exchanging two rows or two columns changes the sign of the determinant.
- Adding one row to another, or one column to another column, does not change the determinant.
- Multiplying a row or a column by a number changes the value of the determinant by the same factor.
For a \(2\times 2\) determinant, we have
\( \left |\begin{array}{cc} a & b \\ a & b \end{array}\right | = 0. \)
\( \left |\begin{array}{cc} a & b \\ c & d \end{array}\right | = - \left |\begin{array}{cc} c & d \\ a & b \end{array}\right |. \)
\( \left |\begin{array}{cc} a & b \\ c & d \end{array}\right | = \left |\begin{array}{cc} a & b \\ a+c & b+d \end{array}\right |. \)
- \( \left |\begin{array}{cc} \lambda a & \lambda b \\ c & d \end{array}\right | = \lambda \left |\begin{array}{cc} a & b \\ c & d \end{array}\right |. \)
As a consequence, if \(a\ne 0\),
\( \left |\begin{array}{cc} a & b \\ c & d \end{array}\right | = \left |\begin{array}{cc} 1 & b/a \\ 0 & ad-bc \end{array}\right |, \)
which is a combination of "row operation". All five properties are shared by \(3\times 3\) and higher dimension (defined shortly) determinants. For \(a_{11}\ne 0,\) the row operation 5 shows how to vanish all the other terms in the first column. By this means, calculations of the value of a \(N\times N\) determinant are reduced to computing a \((N-1)\times (N-1)\) determinant, and the procedure begs to be repeated, leaving eventually a single number - the sought value of the determinant. (Naturally, there are also "column operations" with similar properties and effects.)
Determinants are defined for all \(N\times N\) square matrices \(M = (a_{ij})\):
\[ \left | M \right | = \sum_{\sigma \in S_n} sign(\sigma) \prod_{i=1}^N a_{i,\sigma_i},\ \]
where \(S_n\) is the group of all permutations of the set \(\{1, 2, ..., N\}\), \(\sigma_i\) is the image of \(i\) under the permutation \(\sigma\), and \(sign(\sigma)=\pm 1\) depending on whether \(\sigma\) is even or odd.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
71536481
