Area of Parallelogram Formula by Shearing

This is a well known fact in linear algebra that a \(2\times 2\) determinant \(\left| \begin{array}{cc} a & b \\ c & d \end{array} \right| = ad - bc\) defines the signed area of the parallelogram on two vectors \(\left( \begin{array}{c} a \\ c \end{array} \right)\) and \(\left( \begin{array}{c} b \\ d \end{array}\right)\).

The proof below employs the shearing transform that slides a shape between parallel lines. According to Euclid's Elements I.35 - I.38, shearing preserves areas in triangles and parallelograms.

So we start with a configuration defined with a parallelogram on four point: \((0,0)\), \((b,d)\), \((a,c)\), and \((a+b,c+d)\).

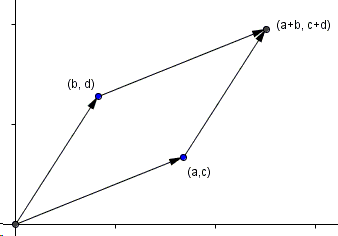
The line through the latter two points has the parametric equation \(f(t)=(a,c)+t(b+d)\) and meets the \(x\)-axis in point \((a-bc/d,0)\).

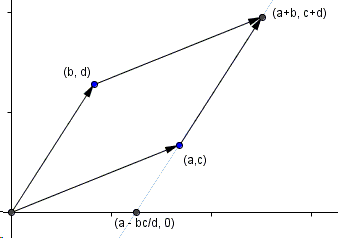
Shearing along that line does not change the area of the parallelogram. The upper edge of the resulting parallelogram is now parallel to the \(x\)-axis. Its extension meets the \(y\)-axis in point \((0, d)\).

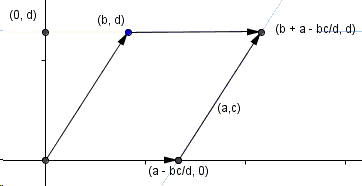
A second shearing leads to a rectangle with sides \(a-bc/d\) and \(d\).

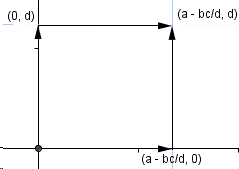
The area of the rectangle (as also that of the original parallelogram) equals \(d \times (a-bc/d) = ad-bc\), as required.

What Is Shear Transform?

• Shearing Butterflies in Quadrilaterals
• Area of Parallelogram Formula by Shearing
• Parallelogram and Ellipses
• Proof 37 of the Pythagorean theorem - by David King
• Shearing a Polygon into a Triangle of Equal Area
• Pythagoras' Theorem By Sheer Shearing
• Shearing and Translation in Pythagorean Pants

|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny