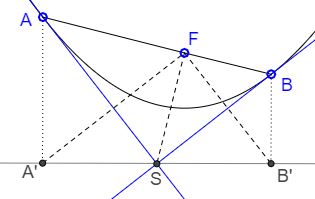
Two Tangents to Parabola

Assume there are two points A and B on a parabola, with tangents AS and BS meeting in S. A' and B' are the feet of perpendiculars from A and B to the directrix of the parabola. Then

S is the circumcenter of ΔA'B'F,
∠FAS = ∠FA'B' = ∠FSB,
∠FBS = ∠FB'A' = ∠FSA,
Triangles BFS, SFA, and B'FA' are similar,
F lies on AB iff S lies on A'B' and, in this case, ∠ASB = 90^o.

Proof

From the reflective properties of parabola, SA is the perpendicular bisector of FA'. Therefore, SA' = SF. Similarly, SB' = SF.
An inscribed angle FA'B' and a central angle FSB' subtend the same chord. Hence,

∠FSB = ∠FSB'/2 = ∠FA'B'.

On the other hand, angles FA'B' and SAA' have pairwise perpendicular legs and are thus equal. Since, ∠SAA' = ∠FAS,

∠FA'B' = ∠FAS.
Similar to 2.
Follows from 2-3. Triangles BFS, SFA, and B'FA' have the same orientation and are directly similar. Triangles SA'A and BB'S are also similar the above three, but have a different orientation.
To shorten the expressions, let's introduce α = ∠FAS and β = ∠FBS. If S lies on the directrix, 2(α + β) = 180°. Then ∠AFS = (90° - α) + (90° - β) = 90°, and similarly ∠BFS = 90°. So AFB is a straight line. The argument is obviously reversible.

The latter property is often referred to as orthoptic:

Two tangents to a parabola are perpendicular iff their point of intersection lies on the directrix.

References

H. Dörrie, 100 Great Problems Of Elementary Mathematics, Dover Publications, NY, 1965

Conic Sections > Parabola

72365767