Cutting Triangles off Regular Hexagon

Given a regular hexagon. Join the midpoints of successive sides. This creates a second hexagon. Find the relation between the areas of the two hexagons.

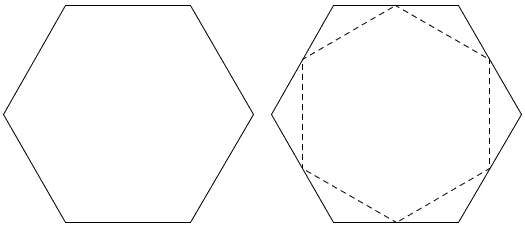
I came across this problem at the site of St Ann's School at Brooklyn where I went after reading Paul Lockhart's A Mathematician's Lament. The problem was accompanied by an animated solution found by a group of students.

The kids solved the problem by an engaging dissection that well qualified to be regarded as a proof without words.

Solution 1

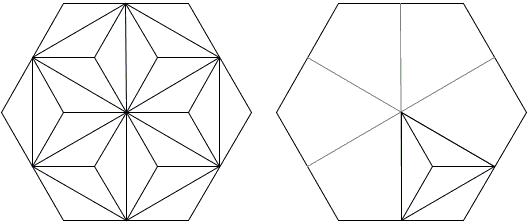
The kids chopped the hexagon into 24 equal triangle of which 18 compose the smaller hexagon, making the ratio of the areas 18/24 = 3/4, with 1/4 of the original area cut off. (First join the midpoints to the center of the hexagon to obtain 6 equilateral triangles. In each of these, join the center with the vertices. On the right you see the minimal configuration that explains the solution.)

(This solution was also included in C. W. Trigg's Mathematical Quickies, Dover, 1985, #75.)

The central symmetry of both the hexagon and the equilateral triangle assisted by simple angle calculations go a long way to justify this solution. The final design is quite attractive and carries a significant esthetic appeal. The problem caught my eye. The mathematics needed to comprehend the problem, come up with and explain the solution was minimal. I immediately thought of Lockhart's remark p. 24). If there anything like a unifying principle in mathematics, it is this: simple is beautiful.

In mathematics, simplicity is often relates to the principle of economy, also known as Occam's Razor after the 14th century logician and Franciscan friar William of Ockham, Ockham being a village in the English county of Surrey. The principle states that

Entities should not be multiplied unnecessarily.

This of course admits multiple interpretations. One is, whenever possible, reduce the problem at hand to a simpler or an already solved one. A relevant candidate problem here could be to consider a triangle with the midpoints of the sides joined. In any triangle, this operation dissects the triangle into 4 equal ones. The configuration is simple but the argument requires some knowledge of proportions and similarity. It actually could be a good starting point for those topics. In any event, it leads to

Solution 2

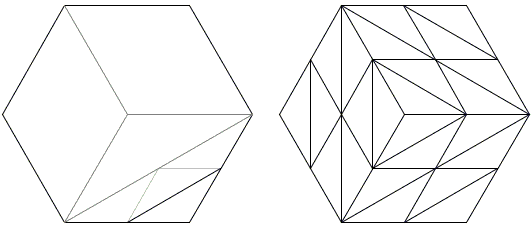
The hexagon is first cut into 3 equal rhombi which often go under the name of lozenges and appear in this configuration in a very appealing problem. One of these is divided into two equal triangles with the area one sixth of the area of the hexagon. One of the cut-off triangles is one forth of this by the aforementioned problem. (On the right, you can see a related dissection.)

Now, as the problem was clearly intended for budding geometry fans, I offered it to my 6-grader son, Eli (turning 11 in a couple of weeks). He came up with

Solution 3

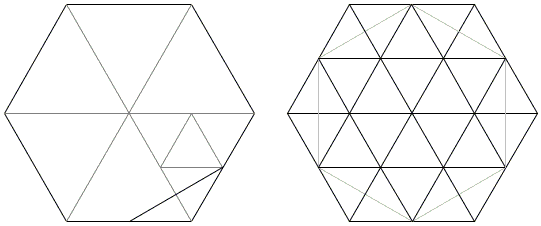
Cut the given hexagon by three long diagonals into six equilateral triangle and then split one of these into 4 smaller ones, as we mentioned above. Each of the small triangles consists of two halves which, if combined differently, also form a cut-off triangle in the original problem. The supporting argument here needs only to appeal to the inherent symmetries of the hexagon and the equilateral triangle. (On the right, you can see a related dissection.)

Bui Quang Tuan came up with a fourth solution that employs similarity very much in the spirit of Euclid VI.31.

Solution 4

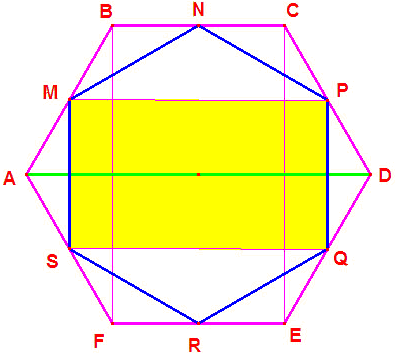
Suppose, ABCDEF is regular hexagon and M, N, P, Q, R, S are midpoints of AB, BC, CD, DE, EF, FA. Of course, by similarities,

Area(ABCDEF)/Area(MNPQRS) = Area(BCEF)/Area(MPQS)

In ΔABF, MS = BF/2. In the trapezoid ABCD: MP = (AD + BC)/2 = 3·BC/2. Therefore,

Area(ABCDEF)/Area(MNPQRS) = Area(BCEF)/Area(MPQS) = BF·BC/(MS·MP) = 4/3.

Solution 4'

In a subsequent mail Bui Quang Tuan has observed that there is no need to invoke similarity.

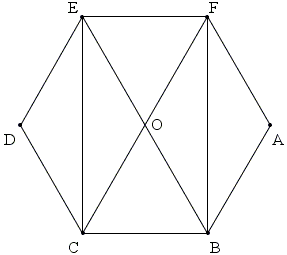
As can be seen from the diagram, Area(ABCDEF)/Area(BCEF) = 3/2, because the diagonal of a rectangle cut it into four parts of equal area. Similarly, Area(MNPQRS)/Area(MPQS) = 3/2. We thus have Area(ABCDEF)/Area(MNPQRS) = Area(BCEF)/Area(MPQS) without recourse to similarity. From here the argument proceeds as in Solution 4.

Thus Solution 4 can be upgraded to avoid the similarity argument. However, the reference to Euclid VI.31 brought to mind another solution.

Solution 5

With the reference to the previous diagram, let O be the common center of the two hexagons. By the similarity, Area(ABCDEF)/Area(MNPQRS) = AO²/MO². But from ΔAOM, MO/AO = cos(∠AOM) = cos(30°) = √3/2. It follows that

Area(ABCDEF)/Area(MNPQRS) = (2/√3)² = 4/3.

Relative to hexagon ABCDEF, lines OM, ON, ... are called apothemes. These are the perpendiculars from the center of the hexagon to the sides. For the sake of a proof, we could have used - with the same degree of success - the ratio of the apothemes in the two hexagons. MO then would have been one of them.

Solutions 4 and 5 are less innocent, I would say. After all, Euclid postponed the similarity argument until book VI, while discussing an apparently more involved proof of the Pythagorean theorem in Euclid I.47. A possible interpretation of that is that the similarity argument (as regard the areas) requires more sophistication than those based on dissection. However, if nothing else, the proofs underscore the simplicity of the problem.

Solution 6

Bui Quang Tuan has found an additional view to observe the configuration from.

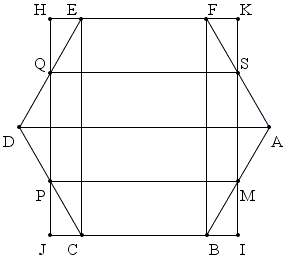
Find points I, J, H, K at the intersection of lines MS and PQ with BC and EF. Note the small equal triangles and observe that

Area(ABCDEF) = Area(IJHK),

on one hand, and

Area(IJHK) = 2·Area(MPQS),

on the other. As we have seen in Solution 4', Area(MPQS) = 2/3·Area(MNPQRS). So that again Area(ABCDEF) = 4/3· Area(MNPQRS).

Solution 7

Bui Quang Tuan also found that the ratio 4/3 is preserved for hexagons that are not regular. All that is required is central symmetry. The proof appears on a separate page.

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny