Tiling a Triangulated Hexagon
A hexagon is cut out of a triangular grid. You have a supply of rhombi the size of two adjacent grid triangles with which to tile the hexagon. The rhombi come in three varieties each associated with one of the three directions of the common side of their constituent grid triangles. Prove that if the rhombi tile the whole hexagon, there is exactly the same number of rhombi of each variety.
Instead of tiling the hexagon with rhombi, we may think of splitting it into pairs of adjacent triangles. An easy way to do that is to join the centers of any two paired triangles. In the applet below, click on one of the triangles and then move (not drag) the cursor to the other one and click there too. The lines joining the centers may have one of three directions. When no single triangle is left over, there are as many lines in one direction as in any other.
| What if applet does not run? |
This problem was posted by Guy David and Carlos Tomei in the Proofs Without Words section of the American Mathematical Monthly (v. 96, no. 5, May 1989, pp. 429-430). It was reprinted in [Proofs Without Words, p. 142] and in a concise form in [Winkler, p. 46]. An extended discussion can be found in [The Art of Mathematics, #24].
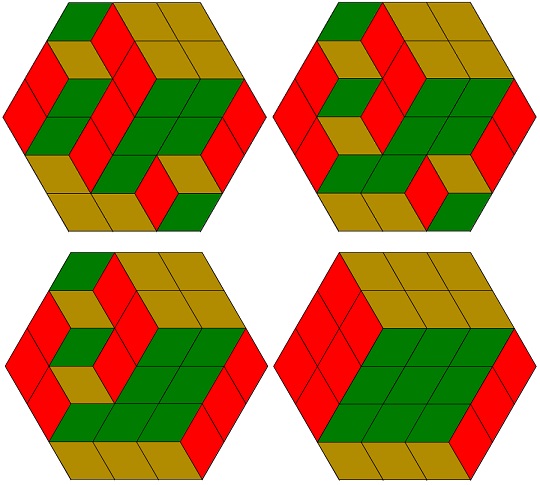
Below is the one used originally by David and Tomei. The idea I believe is just to see in that a 3d configuration of unit cubes. Bollobas starts the first of the three proofs in his book with the question: "Look at the tiling. What do you see?" If you can recognize a 3d configuration, the rest is simple: imagine looking at the shape from three directions: from above (or below, depending on what you see), from left and right. In you mind's eye you should see $N\times N\,$ square with all square cells the same color. That's the proof.
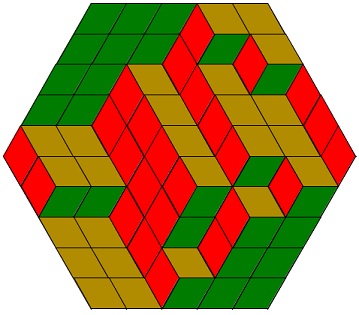
I have accepted that proof and the reliance on my visiual perception from the moment I saw it in Nelsen's book. However, while I played with the applet, I would run time and again into ambigously looking configurations, explained by the oddity related to the orthographic projection. This is of the kind encountered in the cube or counting cubes illusions. The phenomenon also appears as the Necker Cube illusion. What you see depends very much on the adopted point of view which is liable to shift from moment to moment.
For example, it takes me an effort to see anything realistic in the configuration at the low right corner. Usually I see there an impossible shape. It could be a legitimate question to ask whether a realistic configuration, i.e., that is the perceived vision of up/down and left/right, is always possible. Other proofs in [Bollobas, 79-82] confirm that this is so.
The problem has been motivated by the form of a French candy and the shape of the box it is usually sold in:
A calisson is a French sweet that looks like two equilateral triangles meeting along an edge. Calissons could come in a box shaped like a regular hexagon, and their packing would suggest an interesting combinatorial problem. Suppose a box with side length n is filled with sweets of sides 1. Calissons could be placed in three different directions. Prove that a filled out box contains as many calissons in one direction as in any other.
References
- B. Bollobás, The Art of Mathematics: Coffee Time in Memphis, Cambridge University Press, 2006
- R. B. Nelson, Proofs Without Words, MAA, 1993
- P. Winkler, Mathematical Puzzles: A Connoisseur's Collection, A K Peters, 2004
|Activities| |Contact| |Front page| |Contents| |Games|
Copyright © 1996-2018 Alexander Bogomolny73572734
