A Property of Centrally Symmetric Hexagons

Regular hexagons have a property that cutting off the triangles obtained by joining the midpoints of consecutive sides leaves a hexagon of 3/4 of the area. Bui Quang Tuan has observed that the same property holds more generally for all centrally symmetric hexagons:

Given a centrally symmetric hexagon. Join the midpoints of successive sides. This creates a second hexagon. The ratio of the areas of the two hexagons is 4:3.

Solution 1

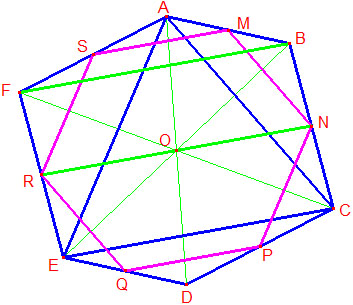
central hexagon with the midpoints of successive sides joined

Observe that in a centrally symmetric hexagon the opposite sides are necessarily parallel and equal in length; also the three diagonals each pass through the center of symmetry and are divided by the center in halves.

Successively, in the triangles CEF, ACD, and ADE,

	Area(OCE)	= Area(OEF)
	Area(OAC)	= Area(OCD)
	Area(OAE)	= Area(OED)

Summing up, Area(ACE) = Area(FEDC) = Area(ABCDEF)/2. It follows that

(1)

Area(ABCDEF) = 2·Area(ACE)

In the trapezoid SMNR, SM = FB/2 = EC/2, RN = EC. Further,

Distance from SM to FB = 1/2 Distance from A to FB,
Distance from FB to RN = 1/2 Distance from FB to EC.

Therefore, Distance from SM to RN = 1/2 Distance from A to EC and

Area(SMNR)=3/4·Area(ACE).

We also have Area(SMNR) = Area(MNPQRS)/2 so that

(2)

Area(MNPQRS) = 2·Area(SMNR) = 3/2·Area(ACE).

From (1), (2) we have the required result: Area(ABCDEF) / Area(MNPQRS) = 4/3.

However, this is not the end of the story. The story keeps unfolding. Bui Quang Tuan has improved on his previous proof.

Solution 2

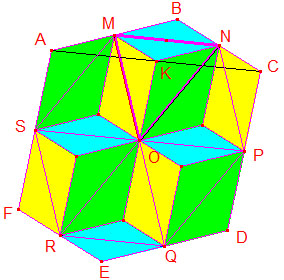
central hexagon with the midpoints of successive sides joined. #2

Let K denote the midpoint of AC. Triangle MNO is split into three smaller ones for which we easily get three congruences:

ΔKNO = ΔAMS
ΔKMO = ΔCNP
ΔKMN = ΔBNM.

We may treat similarly triangles ONP, OPQ, OQR, ORS, OSM, as in the diagram, where all triangles of same color are congruent.

On counting the congruent triangles we immediately have the required

Area(ABCDEF) / Area(MNPQRS) = 4/3.

71940090