A Problem of Acute Triangle
The following problem by Marian Dinca has been posted by Leo Giugiuc at the CutTheKnotMath facebook page. Leo later supplied a solution in complex numbers and coordinate geometry. Below is a slightly modified form of Leo's solution.
Point $P$ is in the interior of $\Delta ABC.$
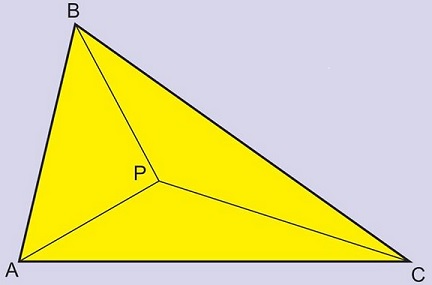
Prove that the lengths $AB+PC,$ $AC+PB,$ $BC+PA$ are the sides of an acute triangle.
With a reference to the condition induced by the Law of Cosines for a triangle to be acute, Leo formulated an equivalent problem:
Let $u,\,v,\,w$ be complex (not collinear) numbers; $p=\alpha u+\beta v+\gamma w,$ where $\alpha,\,\beta,\,\gamma$ are positive real numbers, $\alpha +\beta +\gamma=1.$ Then
$\left(|p-v|+|w-u|\right)^{2}+\left(|p-w|+|u-v|\right)^{2}\gt \left(|p-u|+|v-w|\right)^{2}.$
Proof
By the triangle inequality,
$|p-v|+|w-u|\ge |(p-v)+(w-u)|=|(p-u)-(v-w)|\\ |p-w|+|u-v|\ge |(p-w)-(u-v)|=|(p-u)+(v-w)|.$
It follows that
$\begin{align} \left(|p-v|+|w-u|\right)^{2}&+\left(|p-w|+|u-v|\right)^{2}\\&\ge \left(|(p-u)-(v-w))|\right)^{2}+\left(|(p-u)+(v-w)|\right)^{2}\\ &=2\left(|p-u|^{2}+|v-w|^{2}\right), \end{align}$
the latter by the Parallelogram Law. But
$2\left(|p-u|^{2}+|v-w|^{2}\right)\ge \left(|p-u|+|v-w|\right)^{2}$
which almost proves the required inequality. We need only to show that the inequality is strict, i.e., that the equality is not possible. Assuming otherwise, we'd need to have
$|p-v|+|w-u|= |(p-v)+(w-u)|\\ |p-w|+|u-v|= |(p-w)-(u-v)|.$
However, either leads to a contradiction. E.g., the first means that $p-v=\lambda (w-u),$ for a real $\lambda.$ This would imply $\alpha=-\lambda,$ $\beta=1,$ $\gamma=\lambda.$ However, by the conditions of the problem, all three $\alpha,$ $\beta,$ and $\gamma$ are positive and less than $1.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73566294
