Torque as a Mathematical Object
Elsewhere we considered a water tank in the form of a right triangular prism with a right triangle as a base [Mark Levi, p. 10] mounted on a vertical spindle at one of the acute angles of the base triangle. The prism could freely rotate around the spindle. The fact that it did not was found to be equivalent to vanishing of the net torque (due to the pressure of water in the tank) which, in turn, was equivalent to the Pythagorean theorem.
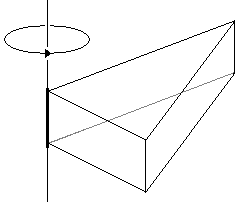
Here we shall place the zero-torque condition into a mathematical framework which would be actually equivalent to the one used in other "Calculus proofs", like #40 and #90.
We start with a geometrical statement that the area of a right triangle that rotates around one of its vertices is independent of the angle of rotation. If \(S(\theta)\) is the area of the triangle at angle \(theta\) from its original position then we expect
\[ S'(\theta) = 0. \]
With the help of Calculus shall demonstrate that
\[ S'(\theta) = a\cdot\frac{a}{2}+b\cdot\frac{b}{2}-c\cdot\frac{c}{2} \]
thus making \(S'(\theta)\) equivalent to the Pythagorean theorem.
Let the triangle be rotated through a small angle \(\Delta\theta\). The side \(a\) sweeps a sector of area \(\frac{1}{2}a^{2}\Delta\theta\), with a similar expression for \(c\): \(\frac{1}{2}c^{2}\Delta\theta\).
The leg \(b\) executes two motions simultaneously: sliding in its own direction and rotation around its leading end. The sliding contributes nothing to the change in area or to the rate of this change. The rotation is clearly by the same angle \(\theta\), making the contribution \(\frac{1}{2}b^{2}\Delta\theta\) to the rate. (This same argument is employed in deriving the area formula of an annulus.)
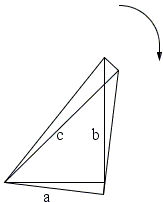
The total area \(\Delta S\) swept by all three sides is
\[ \Delta S = \frac{1}{2}(a^{2}+b^{2}-c^{2})\Delta\theta, \]
where the different signs are explained by the fact that legs \(a\) and \(b\) "consume" the area, pull it under the triangle, or adds it to the triangle's previous position, while the area is "lost" from under the hypotenuse \(c\), i.e., it is subtracted from the triangle's previous position. Dividing by \(\Delta\theta\) and letting \(\Delta\theta\rightarrow 0\), we obtain
\[ S'(\theta) = \frac{1}{2}(a^{2}+b^{2}-c^{2}). \]
We use the same argument elsewhere. The essential point is that if a motion can be split into two independent components, their contributions could be considered independently. During a linear motion the longitudinal contribution to sweeping the area is \(0\), making all of the area acquisition (or loss) due to the frontal motion.
Stuart Anderson takes this idea a step further by composing the motion of linear pieces, each being a frontal movement of a side of a triangle:
First, consider a triangle moving smoothly around in the plane. The "leading edge" sweeps area under the triangle, while area comes back out from under it at the trailing edge. Clearly, the area coming out and going in are equal, since the area of the triangle is constant. That's the first idea.
Now consider a line segment, translating (i.e. moving but not rotating) around a closed path, so that it returns exactly to its original position. Then if we consider a signed flow of area past the segment, the net flow for the closed path will be zero. (Easy to prove, if necessary, but fairly intuitive.) That's the second idea.
Next, let \(ABC\) be a right triangle with sides \(a\), \(b\), and hypotenuse \(c\). Translate it a distance \(a\) perpendicular to side \(a\), then a distance \(b\) perpendicular to side \(b\), and then a distance \(c\) perpendicular to side \(c\), so that the triangle returns to its original position. In the first motion, an area \(a^2\) sweeps into side \(a\) and out of side \(c\); in the second motion, an area \(b^{2}\) sweeps into \(b\) and out of side \(c\), and in the third motion, an area \(c^{2}\) sweeps into side \(c\) and out of sides \(a\) and \(b\) together. This is according to the first idea. But by the second idea, the area swept in and out of side \(c\) are equal. Therefore \(a^2 + b^2 = c^2\).
(Stuart's ideas are very close to those of Ernst Mach.)
Reference
- M. Levi, The Mathematical Mechanic, Princeton University Press, 2009
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73599136
